Ich habe bereits zwei Blogposts zum Thema verfasst, die Grundlage für diesen Blogpost sind:
- Mit der Poisson-Verteilung Sportwetten berechnen
- Mit der Poisson-Verteilung Over/Under-Wettquoten berechnen
1. Ausgangspunkt: Der erweiterte Spreadsheet
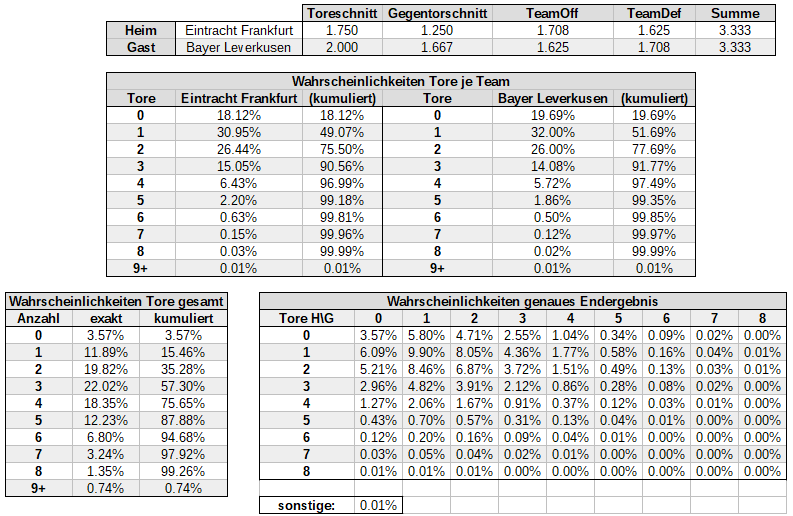
Im Vorgängerpost zur Berechnung von Over/Under-Wettquoten mit Hilfe der Poisson-Verteilung habe ich als Ausgangspunkt einen Spreadsheet verwendet, der auch die Grundlage für diesen Blogpost bildet. Dieser ist auf 8 Tore je Team erweitert und berechnet dementsprechend die Wahrscheinlichkeiten für alle Szenarien, in denen sowohl Team A, als auch Team B 0-8 Tore erzielen, sowie die verbleibende Restwahrscheinlichkeit für die sonstigen Szenarien.
| poisson.vert-naives-modell-sge-vs-b04-final_1_.ods |
2. Erstellung der 1X2-Quoten (Dreiweg) mit der Poisson-Verteilung
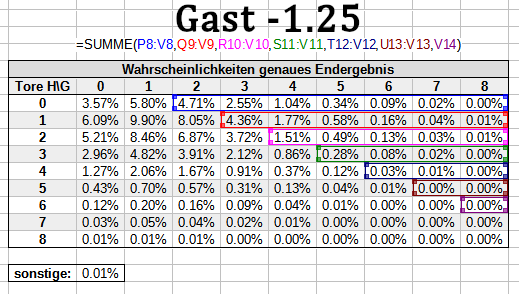
Berechnen wir zunächst die 1X2-Quoten. Dazu ziehst du die Tabelle zu Rate, die die Wahrscheinlichkeiten für jeden einzelnen Spielstand anzeigt.
A. Berechnung der Heimsieg-Wahrscheinlichkeit
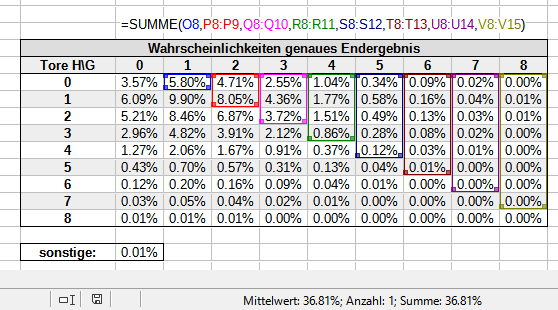
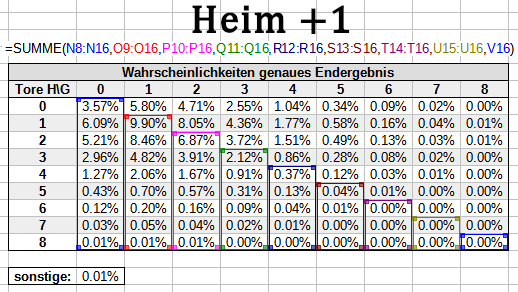
Um die Wahrscheinlichkeit für einen Heimsieg zu erhalten, addierst du die Wahrscheinlichkeiten für alle Szenarien, in denen das Heimteam mit einem oder mehr Toren Abstand gewinnt:
Im Spreadsheet erreichst du das mit dieser Formel:
B. Berechnung der Unentschieden-Wahrscheinlichkeit
Entsprechend gehst du vor, um die Wahrscheinlichkeit für ein Unentschieden zu erhalten. Dazu zählst du einfach alle Spielstände zusammen, in denen beide Teams gleich viele Tore erzielen:
C. Berechnung der Auswärtssieg-Wahrscheinlichkeit
Die Auswärtssieg-Wahrscheinlichkeit wiederum ergibt sich nun (logischerweise) aus allen Szenarien, in denen der Gast mindestens ein Tor mehr erzielt als die Heimmannschaft:
D. Normalisierung der Wahrscheinlichkeiten und Berechnung der Wettquoten
Bitte beachte: Diese Wettquoten sind nicht exakt korrekt, da wir die Restkategorie sonstige nicht berücksichtigt haben. Diese liegt (wie du in der Tortabelle sehen kannst) bei 0.01%[1], und daher kommst du bei den aufsummierten 1X2-Wahrscheinlichkeiten auch nur auf 99.99%, statt auf glatte 100%.
Zwar ist diese Restwahrscheinlichkeit von 0.01% so gering, dass man sie eigentlich vernachlässigen kann. Nichtsdestoweniger ist der korrekte nächste Schritt, die Wahrscheinlichkeiten auf 100% zu normalisieren, und erst aus diesen Werten die Wettquoten abzuleiten. Um die Werte zu normalisieren, teilst du die jeweiligen Wahrscheinlichkeiten für Heimsieg, Unentschieden und Auswärtssieg durch ihre Summe, in diesem Fall also 99.99%.
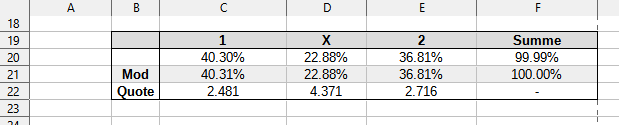
Das Endergebnis für all diese Schritte sieht folgendermaßen aus:
| poisson.vert-naives-modell-sge-vs-b04-erweitert-auf-8-tore-1x2.ods |
3. Asian Handicap Quoten mit der Poisson-Verteilung berechnen
Für die Zwecke dieses Beispiels habe ich mich auf die Berechnung aller Asian Handicap-Linien von -1.5 bis +1.5 beschränkt. Danach sollte klar sein, wie das Prinzip für höhere oder niedrigere Handicaps funktioniert, weil sich darüber hinaus lediglich die Abstände um die entsprechend große Toranzahl verschieben.
Ich habe in diesen Spreadsheet nach langem Überlegen eine Zwischenrechnung eingebaut. Diese ist nicht strikt notwendig, macht den Spreadsheet und die damit verknüpften Formeln aber bedeutend übersichtlicher.
A. Wie du die Quoten berechnen musst: Kurzer Exkurs
Du kannst Wettquoten grundsätzlich mit Brüchen berechnen, und auch im Blogpost zur Berechnung von Over/Under-Wetten mit Hilfe der Poisson-Verteilung habe ich die Vorgehensweise im Kapitel Mit der Poisson-Verteilung Over/Under-Wettquoten berechnen: Grundlagen noch einmal aufgegriffen.
Es ist wichtig, dass du das dahinter stehende Prinzip verstehst. Wenn du die einer Wettquote zugrunde liegenden Wahrscheinlichkeiten in Bruchform berechnest, gelten folgende Regeln:
- Die zusammengezählten Wahrscheinlichkeiten aller Fälle, in denen die Wette gewinnt, kommen in den Zähler.
- Die Summe aller theoretischen möglichen Ausgänge der Wette, in der die Wette entweder gewinnen oder verlieren kann, kommt in den Nenner.
Letzteres wird immer dann relevant, wenn eine Wette ganz oder halb als Push endet, und dementsprechend der ganze oder halbe Einsatz zurückgezahlt wird. Denn wenn für eine Wette der Einsatz zurückbezahlt wird, hat es sie nie gegeben, weshalb das entsprechende Ereignis auch nicht im Nenner berücksichtigt werden darf. Wenn du beispielsweise die fairen Quoten für eine DNB-Wette[2] berechnen willst, darfst du die Unentschiedenwahrscheinlichkeiten nicht in den Nenner einfließen lassen.
Um ganz korrekt zu rechnen, solltest du eigentlich die Restkategorie sonstige in den Nenner einfließen lassen. In diesem Spreadsheet habe ich das aber letztlich nicht getan, weil es deutlich einfacher ist, den Nenner direkt aus der Summe beider Zähler zu berechnen. Da die Differenz nur bei 0.01% Prozentpunkten liegt, ergibt sich daraus kein nennenswerter Unterschied. Beachte aber, dass es zu relevanten Verzerrungen kommen kann, wenn du in deinem Spreadsheet deutlich weniger als acht Tore je Team berücksichtigst.
B. Das Leichteste zuerst: Halbe Handicaps
Halbe Handicaps sind am leichtesten zu berechnen, weil die entsprechende Wette nur gewinnen oder verlieren kann. Entsprechend liegt der Nenner hier automatisch bei 100% - jedes theoretisch denkbare Spielergebnis findet also Platz im Nenner.
Der Nenner bei halben Handicaps
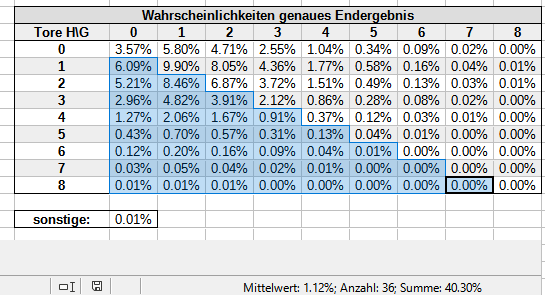
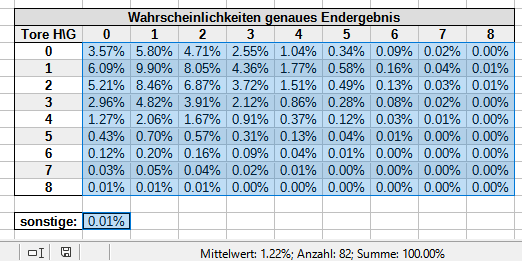
100% bedeutet hier nichts anderes, als dass du wirklich jede einzelne Ergebniswahrscheinlichkeit berücksichtigst, im Spreadsheet also diese blau markierte Fläche (inklusive sonstige).
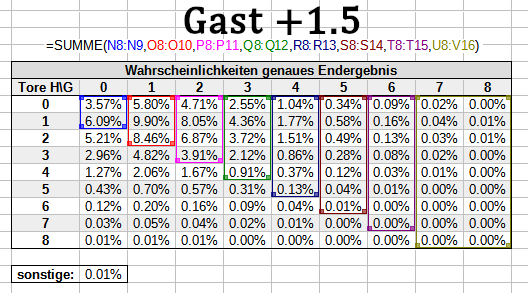
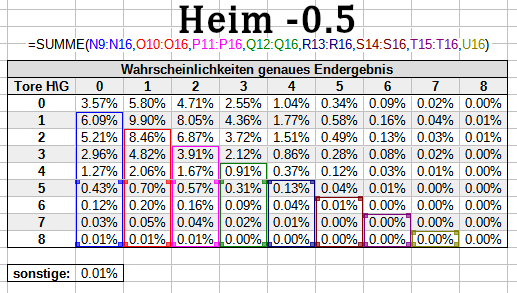
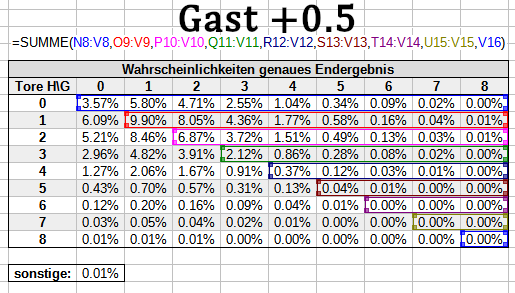
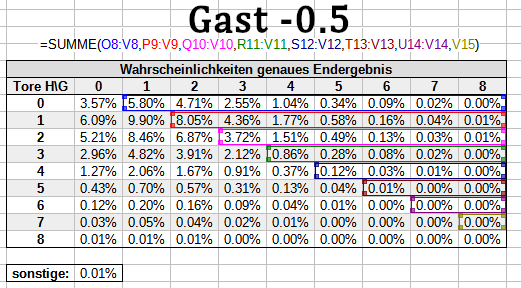
Der Zähler bei halben Handicaps
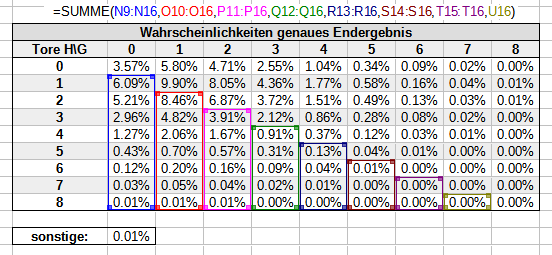
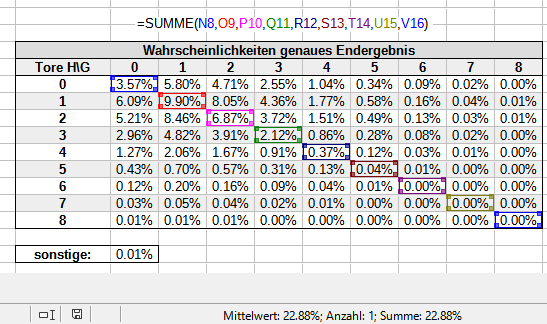
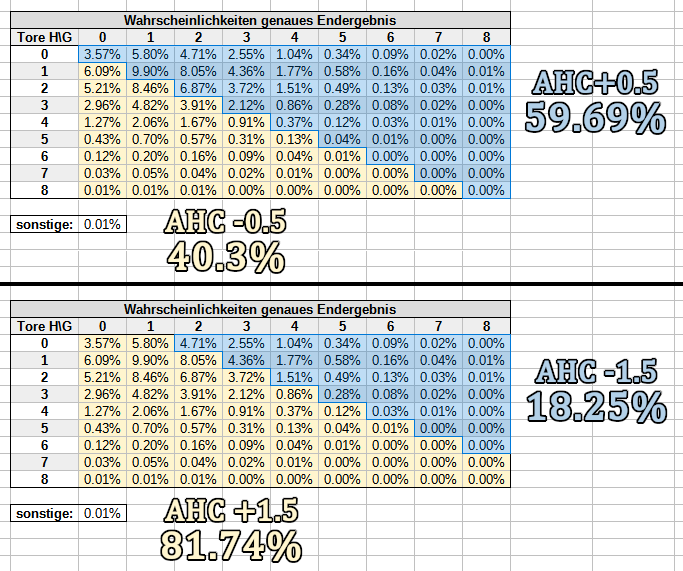
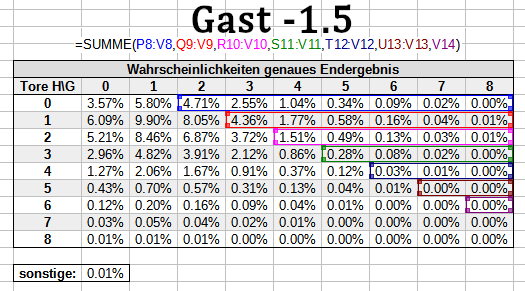
Der Zähler wiederum setzt sich aus allen Wahrscheinlichkeiten zusammen, deren Eintreten zum Gewinn der entsprechenden Wetten führt. Für -0.5/+0.5 und +1.5/-1.5 sieht das beispielsweise so aus:
Bitte beachte: Im Zähler fehlen immer 0.01% auf insgesamt 100%, weil wir für sonstige nicht wissen können, wer die Wette gewinnt. Da der fehlende Betrag aber extrem klein ist, schlägt sich das nur unwesentlich im Gesamtergebnis nieder.
Zwischenrechnung
Nun kannst du die entsprechenden Zähler und Nenner als Formeln in den Spreadsheet einfügen. Die Nenner setzen sich automatisch immer aus der Summe beider Zähler zusammen. Die Zähler kannst du folgendermaßen gestalten:
Normalisierung & Wettquotenberechnung
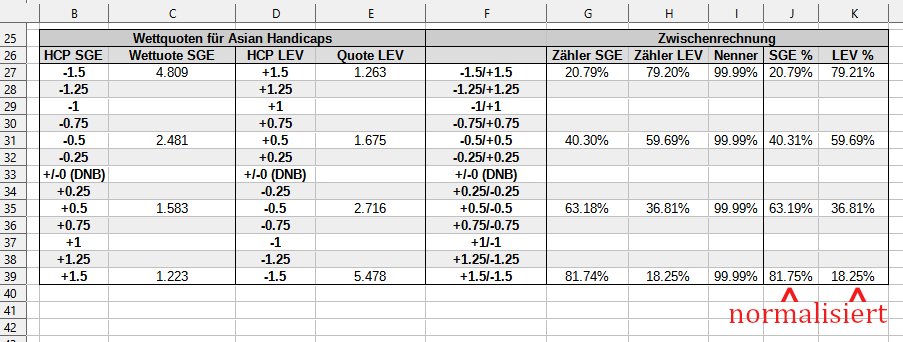
Jetzt normalisierst du die Wahrscheinlichkeiten, in dem du die jeweiligen Zähler durch den Nenner teilst. Bei den halben Handicaps kannst du dir diese Operation im Grunde sparen, weil der Nenner ohnehin bei fast 100% liegt; da du die Normalisierung aber bei allen anderen Handicaps zwingend vornehmen musst, habe ich sie hier ebenfalls durchgeführt, zumal der Spreadsheet dadurch logischer und einheitlicher wird. Im Anschluss kannst du die zugehörigen Wettquoten durch einfache Inversion (1/x) aus den normalisierten Wahrscheinlichkeiten ableiten.
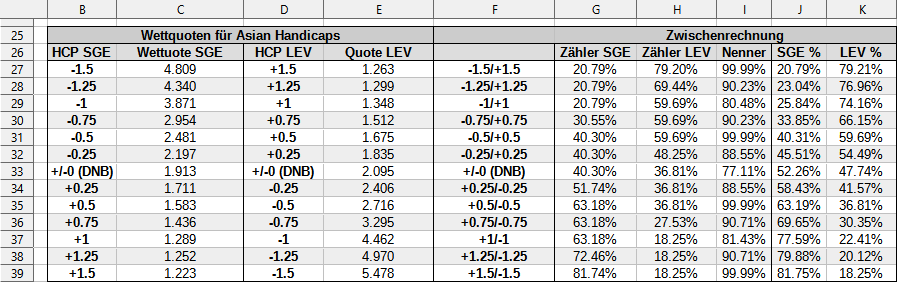
Die normalisierten Wahrscheinlichkeiten findest du in den Spalten J (Heim) und K (Gast), die entsprechenden Wettquoten in den Spalten C und E:
| poisson.vert-naives-modell-sge-vs-b04-erweitert-auf-8-tore-nach-den-halben-ahc.ods |
C. Berechnung der ganzen Asiatischen Handicaps
Für die ganzen Asiatischen Handicaps liegt die Besonderheit der Wettquotenberechnung darin, dass du Spielstände aus den Berechnungen weglässt, nach denen die Wette in zurückgezahlten Einsätzen endet. Beispielsweise also wenn du auf DNB Gast gesetzt hast und das Spiel mit einem Unentschieden endet, oder wenn du auf Heim -1 bist und die Heimmannschaft mit exakt einem Tor Unterschied gewinnt.
Der Nenner
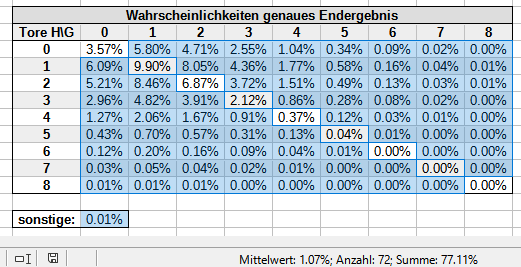
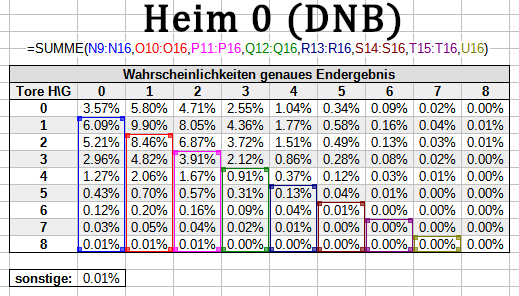
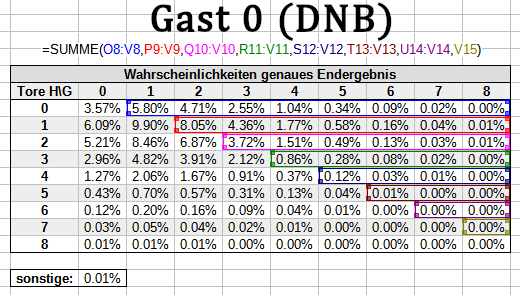
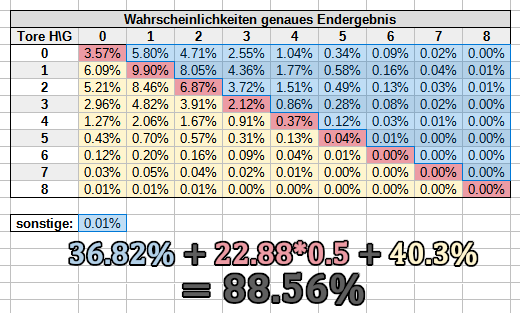
Bei einer DNB-Wette beispielsweise lässt du im Nenner alle Unentschiedenwahrscheinlichkeiten weg - der Nenner erfasst also nur den blauen Bereich, der in der Summe für das Spiel im Spreadsheet 77.11% ergibt:
Der Zähler
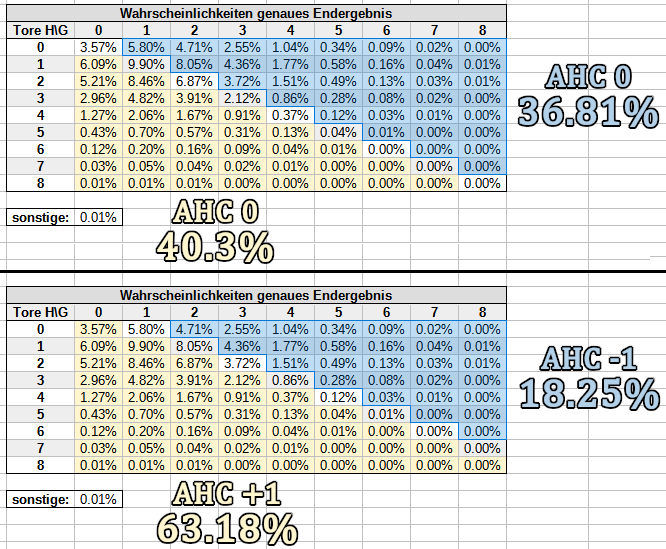
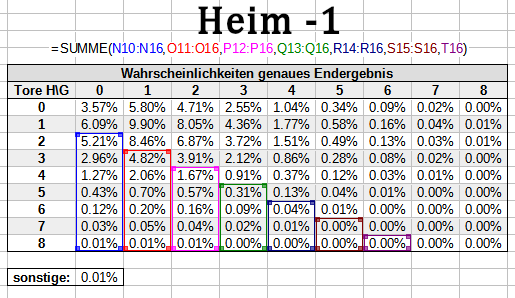
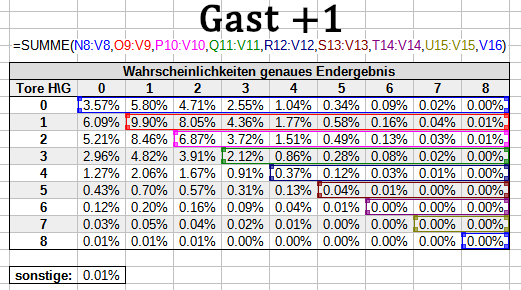
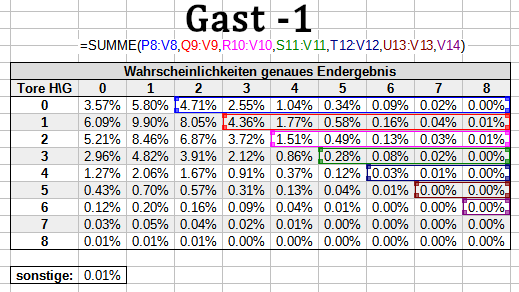
Auch für den Zähler sparst du die entsprechenden Bereiche aus - du berücksichtigst ausschließlich Wahrscheinlichkeiten für Szenarien, in denen die entsprechende Wette gewinnt. So sieht das für das DNB-Handicap und für das +1/-1-Handicap aus:
Zwischenrechnung
Für die Zwischenrechnung verwendest du für die Zähler folgende Formeln für die ganzen Asiatischen Handicaps:
Wie gehabt ermittelst du den Nenner durch die Addition beider Zähler.
Normalisierung & Wettquotenerstellung
Nun normalisierst du wieder die Wahrscheinlichkeiten, indem du sie durch den Nenner teilst. Daraus errechnest du dann erneut durch Inversion (1/x) die korrekten Wettquoten.
D. Berechnung der viertel Asiatischen Handicaps
Viertel Asiatische Handicaps berechnest du so ähnlich wie ganze Asian Handicaps, mit einem Unterschied: In den Szenarien, in denen eine Wette halb gewinnt oder halb verliert (bei +/- 0.25 ist das beispielsweise bei einem Unentschieden der Fall), berücksichtigst du die betreffenden Wahrscheinlichkeiten nur zur Hälfte, während du sie bei ganzen Handicaps komplett ignorierst.
Der Nenner
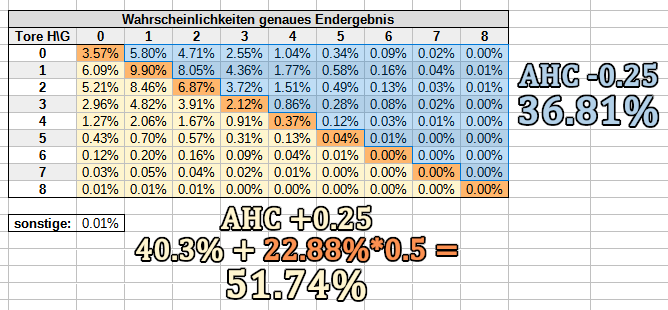
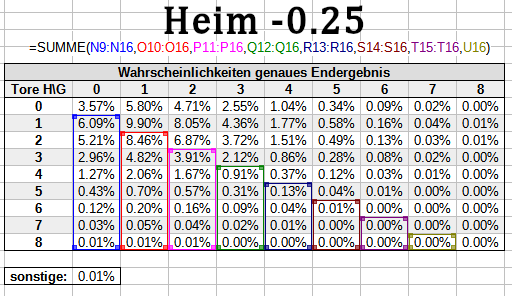
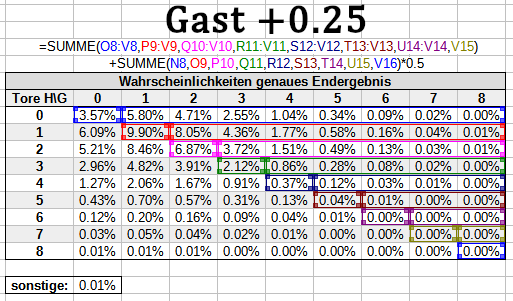
Bei +0.25/-0.25 berücksichtigst du alle Unentschiedenwahrscheinlichkeiten nur zur Hälfte im Nenner, weil die Hälfte der Wette in diesem Fall nicht stattfindet:
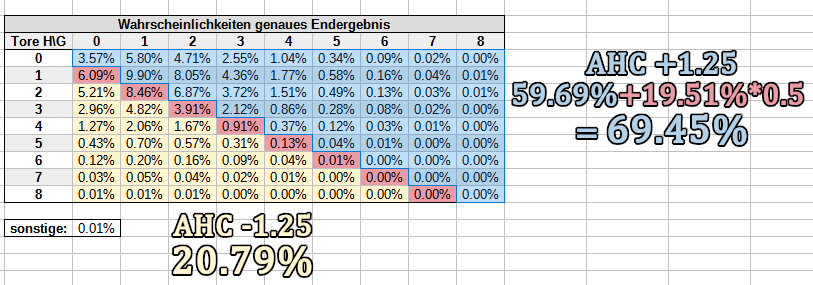
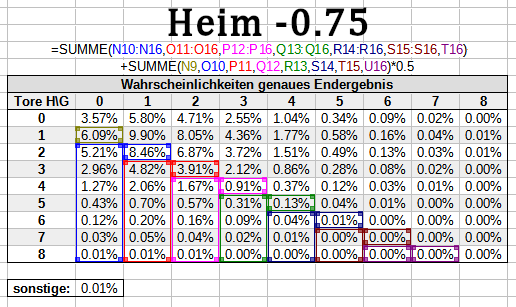
Um die entsprechende Toranzahl verschoben gehst du im Nenner vor, wenn es sich um ein Handicap wie +/-1.25, +/-2.25 etc. handelt. Wenn du beispielsweise den richtigen Nenner für das Heim -1.25 / Gast +1.25 Handicap berechnen willst, halbierst du die Wahrscheinlichkeiten für alle Siege mit einem Tor Vorsprung.
Der Zähler
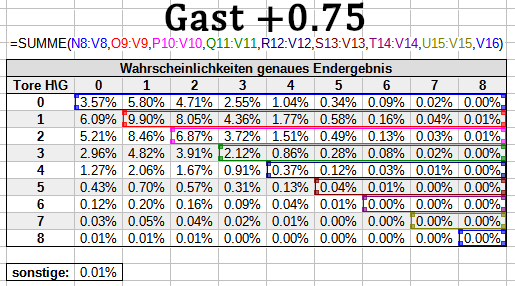
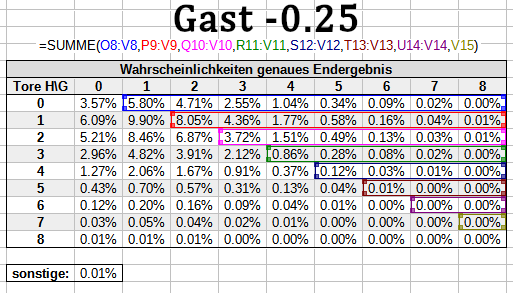
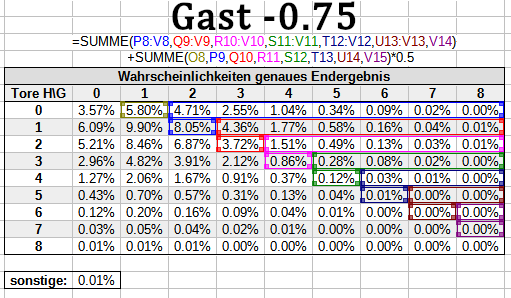
Im Zähler verwendest du alle Wahrscheinlichkeiten, in denen deine Wette komplett gewinnt, wie immer vollständig. Für die Spielausgänge, in denen die Wette nur halb gewinnt, halbierst du die entsprechenden Wahrscheinlichkeiten:
Zwischenrechnung
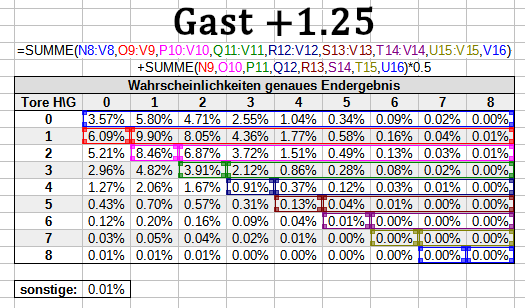
Und folgende Formeln verwendest du im Detail für den Zwischenrechnungsschritt:
Den Nenner kannst du jetzt wieder leicht durch die Addition der beiden Zähler ermitteln.
Normalisierung & Wettquotenerstellung
Nun normalisierst du wieder die Wettquoten indem du sie durch den Nenner teilst, und berechnest daraus deine Wettquoten. Das Endergebnis sollte nun so aussehen:
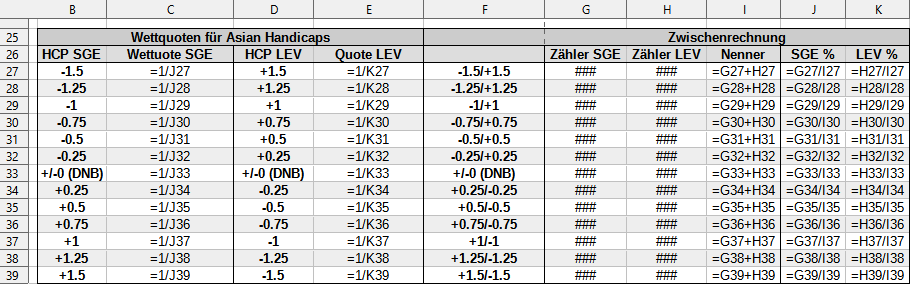
Die selbe Tabelle in ihrer Endfassung auf Formelebene:
Hier findest du die Endfassung des Spreadsheets als Download im .ods-Format:
| poisson.vert-naives-modell-sge-vs-b04-erweitert-auf-8-tore-mit_allen-ahc-finale_datei.ods |
4. Zum Geleit/Ausblick
Ich möchte noch einmal daran erinnern, dass die Poisson-Verteilung und sich daraus ergebende Berechnungen kein Allheilmittel für Sportwetten sind. Das habe ich etwas ausführlicher im Kapitel Die Schwächen der Poisson-Verteilung beim Sportwetten aufgegriffen.
Ferner kann eine Poisson-Verteilung immer nur dann gute Wahrscheinlichkeiten liefern, wenn der Input stimmt. Es ist also wichtig, dass die geschätzten Torerwartungswerte für beide Teams eine solide Grundlage haben. Ist das nicht der Fall, wird nach dem Garbage In/Garbage Out-Prinzip auch am Ende nichts Vernünftiges herauskommen.
Im nächsten Teil werde ich darauf eingehen, wie du die Poisson-Verteilung im Bedarfsfall anpassen kannst, und wie du die Berechnungen für Over/Under und Asian-Handicapquoten in einen Spreadsheet gießt, der eine ganze Saison mit allen Ligaspielen abdeckt.
Fußnoten:
[1] Genau deshalb habe ich die Tormtarix auf acht Tore je Team erweitert: Auf diese Weise ist die Restkategorie verbleibender Ergebnisse insgesamt so unwahrscheinlich, dass man sie im Fußball getrost vernachlässigen kann. Diese Restkategorie wie in diesem Blogpost geschehen bei den Zähler-Berechnungen wegzulassen ist zwar theoretisch nicht ganz sauber, bleibt aber ohne praktische Konsequenzen.
[2] DNB steht für Draw No Bet und ist eine gebräuchliche (und selbsterklärende) Bezeichnung für das asiatische Nullhandicap, bei dem du im Fall eines Unentschiedens deinen Einsatz zurückerhältst.









 RSS-Feed
RSS-Feed