In diesem Teil der Wettmodellserie zeige ich dir, wie du durch die Poisson-Verteilung robuste Schätzungen für deine Wetten ableiten kannst.
Was ist die Poisson-Verteilung eigentlich?
Bei der Poisson-Verteilung handelt es sich um eine diskrete Wahrscheinlichkeitsverteilung, die sich gut für das Modellieren seltener Ereignisse eignet. Beispielsweise ist das Berechnen der Wahrscheinlichkeit dafür, wie viele Tore beide Mannschaften in einem Fußballspiel erzielen werden, eine wesentliche Stärke der Poisson-Verteilung.
Sportwetten bestehen im Fußball zu großen Teilen aus Asian Handicaps und Over/Under-Wetten, und exakt für das Bauen von Wettmodellen in diesen Bereichen kannst du diese Verteilung besonders gut verwenden. Darüber hinaus eignet sie sich auch für das Berechnen der Wahrscheinlichkeit exakter Endergebnisse, also etwa wie wahrscheinlich ein 1-0 für die Heimmannschaft ist.
Inhaltsverzeichnis
Mit der Poisson-Verteilung Sportwetten berechnen: Formel & Vorgehensweise in Excel/Libre Calc
Die Formel der Poisson-Verteilung • Die Poisson-Verteilung mit Excel/Libre Calc berechnen (POISSON.VERT)
Mit der Poisson-Verteilung Sportwetten-Quoten für ein Match vorbereiten: Beispiel
Schritt 1: Offensiv- und Defensivwert für beide Teams errechnen • Schritt 2: Wahrscheinlichkeiten Tore je Team • Schritt 3: Wahrscheinlichkeiten Gesamttorzahl (Over/Under) • Schritt 4: Wahrscheinlichkeiten genaues Ergebnis • Schritt 5: Wahrscheinlichkeiten in Wettquoten umwandeln
Die Schwächen der Poisson-Verteilung beim Sportwetten
1. Die Poisson-Verteilung beruht auf bestimmten Annahmen • 2. Die Poisson-Verteilung beinhaltet keine Buchmachermarge • 3. Dein Output ist nur so gut wie dein Input
Mit der Poisson-Verteilung Sportwetten berechnen: Formel & Vorgehensweise in Excel/Libre Calc
Um mit der Poisson-Verteilung Wahrscheinlichkeiten schätzen zu können, benötigst du für deine Sportwetten zunächst nur eine einfache Information: Wie viele Tore erwartest du im Schnitt?[1] Das kann für das ganze Spiel gelten (also beide Mannschaften) oder ein bestimmtes Team. Mit dieser Information kannst du dann errechnen, wie wahrscheinlich es genau ist, dass eine bestimmte Anzahl Tore fällt.
Die Formel der Poisson-Verteilung
Die Formel der Poisson-Verteilung sieht zwar erst einmal komplex aus, ist mit ein wenig Hintergrundwissen aber im Grunde relativ leicht zu verstehen:
Das wichtigste Element der Formel ist das Lambda (λ), das in allen Modellen mit Torgrundlage für den Torschnitt steht. Wenn du also davon ausgehst, dass der erwartete Torschnitt bei 1.83 liegt, dann gibst du diesen Wert anstelle des Lamdas ein.
Das k steht für die Anzahl der Tore, für die du die Eintrittswahrscheinlichkeit berechnen möchtest. Willst du also wissen, wie wahrscheinlich es ist, dass exakt 2 Tore fallen, ersetzt du das k durch eine 2.
Das Ausrufezeichen steht für Fakultät und das e für die Eulersche Zahl - beides Dinge, die sich mit Hilfe eines Taschenrechners oder Tabellenkalkulationsprogramms leicht ausrechnen lassen.
In diesem praktischen Beispiel für exakt zwei Tore würdest du also so rechnen:
Das Ergebnis dieser Rechnung ist 26.68%, was du für solche Einzelfälle übrigens auch auf verschiedenen Online-Poisson-Rechnern nachrechnen kannst.
Sofern du die Poisson-Verteilung jedoch systematisch einsetzen willst, benötigst du die Hilfe eines Tabellenkalkulationsprogramms.
Die Poisson-Verteilung mit Excel/Libre Calc berechnen (POISSON.VERT)
Du könntest nun diese Formel exakt so in Excel/Libre Calc eingeben[2], allerdings geht das dort auch leichter und eleganter mit der POISSON.VERT-Funktion:
| poisson.vert.ods |
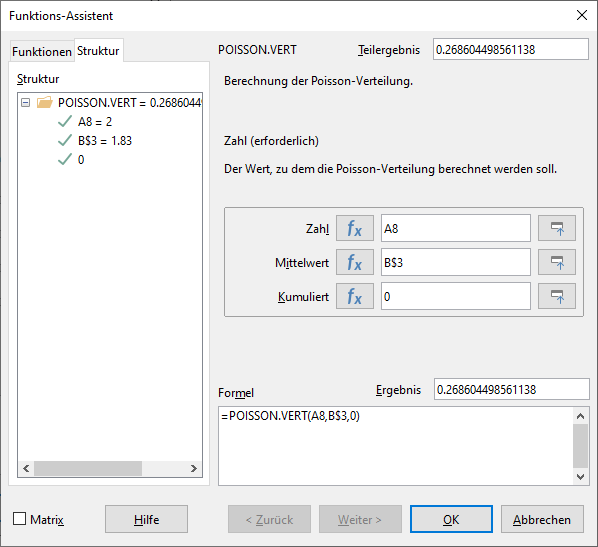
Die POISSON.VERT-Funktion hat drei Komponenten:
- Zahl: dies entspricht dem k der Poissonverteilungsformel, hier also die Anzahl der Tore, für die du die jeweilige Eintrittswahrscheinlichkeit herausfinden möchtest. Mein Beispielspreadsheet deckt 0-5 Tore ab, die sich in den Zellen A6 bis A11 befinden.
- Mittelwert: dies entspricht dem Lambda (λ) der Poissonverteilungsformel. Hier trägst du also entweder den Toreschnitt direkt als Zahl ein, oder aber die Zelle, die den Wert enthält. In meinem Beispielspreadsheet habe ich die Zelle B3 gewählt.
- Kumuliert: Gibst du hier 0 ein, setzt du damit diesen Wert auf “falsch”, was bedeutet, dass du die Wahrscheinlichkeit für exakt k Tore erhältst. Du kannst hier auch eine 1 eingeben, um die Kumulierung zu bejahen. In diesem Fall wird dir die Wahrscheinlichkeit dafür angezeigt, dass die Anzahl der Tore bei k oder weniger liegt. Ist beispielsweise k=2, dann erhältst du die aufaddierten Wahrscheinlichkeiten für exakt 0, 1 oder 2 Tore.
Du findest im Spreadsheet darüber hinaus auch noch in Zeile 12 die Option 6+ Tore. Die Wahrscheinlichkeit daraus errechnet sich aus der Gegenwahrscheinlichkeit zur kumulierten Wahrscheinlichkeit von 5 oder wenigen Toren, hier also aus 100% - 98.88% = 1.12%. Du kannst natürlich prinzipiell beliebig weit höher gehen mit der Toranzahl, allerdings ergibt das aufgrund der sehr niedrigen Wahrscheinlichkeiten ab einem bestimmten Punkt nur wenig Sinn. Persönlich lasse ich es meistens bleiben, sobald die Restwahrscheinlichkeit bei weniger als einem Prozentpunkt liegt.
Mit der Poisson-Verteilung Sportwetten-Quoten für ein Match vorbereiten: Beispiel
Zeit für ein praktisches Beispiel. Hier nehme ich die am Freitag anstehenden Partie des 8. Spieltags der Saison 2019/20 zwischen Eintracht Frankfurt und Bayer Leverkusen. Als Grundlage dient mir ein naives Tormodell, das einfach nur berücksichtigt, wie viele Tore beide Teams im Schnitt zu Hause bzw. auswärts bisher erzielt haben, und wie viele Tore sie dabei zugelassen haben[3]. Für die Berechnungen hier verwende ich folgende Daten, Stand nach dem 7. Spieltag 2019/20:
- Durchschnittliche Heimtore pro Spiel für Eintracht Frankfurt: 1.750
- Durchschnittliche Heimgegentore pro Spiel für Eintracht Frankfurt: 1.250
- Durchschnittliche Auswärtstore pro Spiel für Bayer Leverkusen: 2.000
- Durchschnittliche Auswärtsgegentore pro Spiel für Bayer Leverkusen: 1.667
Schritt 1: Offensiv- und Defensivwert für beide Teams errechnen
Um für dieses Spiel den erwarteten Torwert für Eintracht Frankfurt zu berechnen, addierst du zunächst den Heimtorschnitt Frankfurts und den Gegentorschnitt Leverkusens, und teilst diesen Wert durch zwei. Genauso verfährst du mit dem Auswärtstorschnitt Leverkusens und dem Heimgegentorschnitts Frankfurts, um den erwarteten Torwert für Bayer Leverkusen zu erhalten:
| Team | Torschnitt | Gegentorschnitt | Offensiv | Defensiv | Summe |
|---|---|---|---|---|---|
| Eintracht Frankfurt (H) | 1.750 | 1.250 | 1.708 | 1.625 | 3.333 |
| Bayer Leverkusen (A) | 2.000 | 1.667 | 1.625 | 1.708 | 3.333 |
Hier kannst du diese Ausgangsposition im .ods-Format für Libre Calc herunterladen:
| poisson.vert-naives-modell-sge-vs-b04-tore-je-team-start.ods |
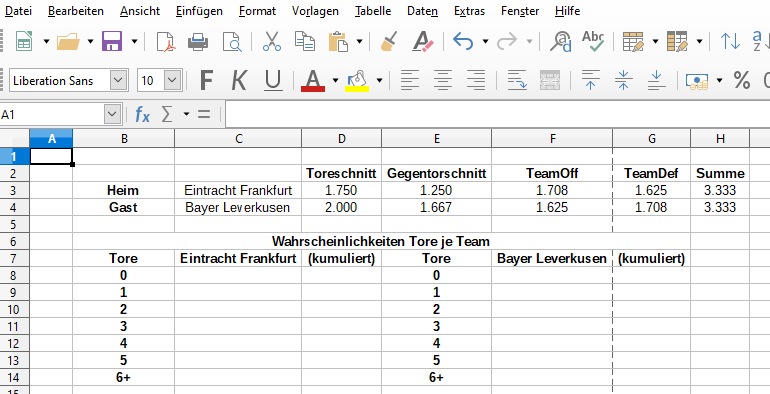
Schritt 2: Wahrscheinlichkeiten Tore je Team
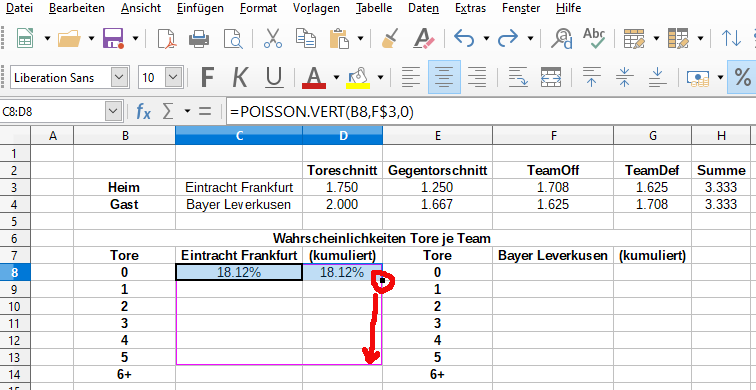
Nun berechnest du die Wahrscheinlichkeiten der spezifischen Toranzahlen für beide Teams. Verwende dazu für Eintracht Frankfurt folgende Formeln in den Zellen C8 und D8:
- C8: =POISSON.VERT(B8,F$3,0)
- D8: =POISSON.VERT(B8,F$3,1)
Die Formeln sind nahezu identisch. Der einzige Unterschied besteht in der 0 und der 1, was bewirkt, dass in Spalte C die exakten Wahrscheinlichkeiten für die entsprechenden Toranzahlen angezeigt werden und in Spalte D die kumulierten Wahrscheinlichkeiten. Das Dollarzeichen dient der Konstanthaltung der entsprechenden Zahl.
Ziehe beide Formeln bis Zeile 13 hinunter, um die restlichen Zellen automatisch aufzufüllen:
Um in Zeile 14 die Wahrscheinlichkeit für 6 oder mehr Tore zu errechnen, benötigst du die Gegenwahrscheinlichkeit von 5 oder weniger Toren, was du beispielsweise so berechnen kannst:
- C14: =1-SUMME(C8:C13)
- D14: =1-D13
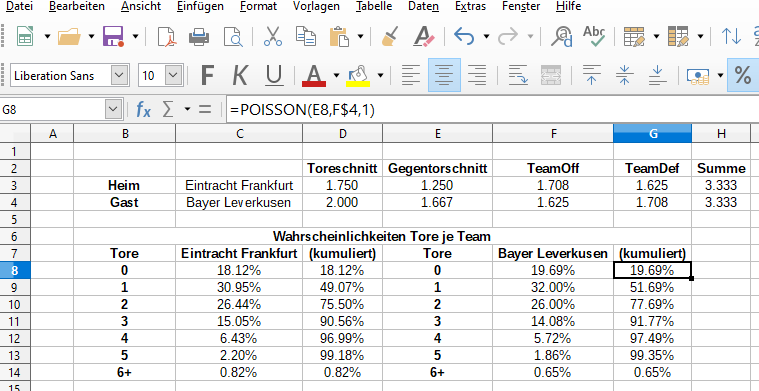
Wenn du den gesamten Vorgang für Bayer Leverkusen mit den entsprechenden Anpassungen wiederholst, sollte das Ergebnis so aussehen:
| poisson.vert-naives-modell-sge-vs-b04-tore-je-team-fertig.ods |
Schritt 3: Wahrscheinlichkeiten Gesamttorzahl (Over/Under)
Wenn du die erwarteten Tore je Team aufaddierst, wie in Zelle H3 und H4 geschehen, kannst du ausgehend von dieser Zahl auch berechnen, mit welcher Wahrscheinlichkeit du wie viele Tore insgesamt in der Begegnung erwartest. Dies bildet die Grundlage für Over/Under-Wetten.
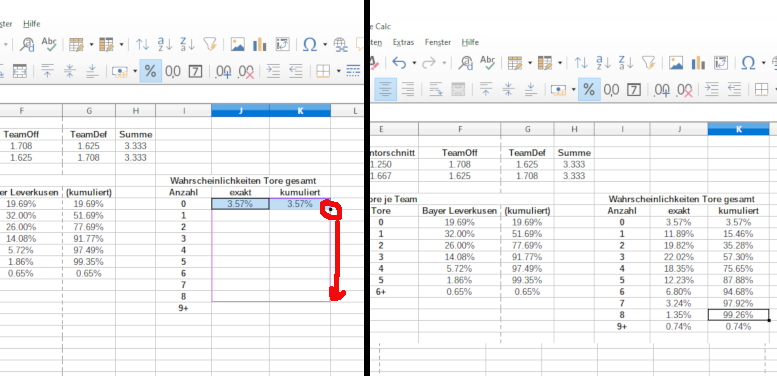
Du verwendest dazu folgende Formeln in den Zellen J8 und K8:
- J8: =POISSON.VERT(I8,H$3,0)
- K8: =POISSON.VERT(I8,H$3,1)
Nach den gleichen Schritten wie zuvor landest du bei folgendem Endergebnis:
| poisson.vert-naives-modell-sge-vs-b04-tore-gesamt-over-under.ods |
Schritt 4: Wahrscheinlichkeiten genaues Ergebnis
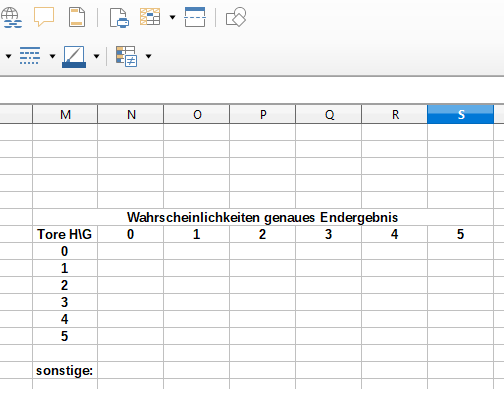
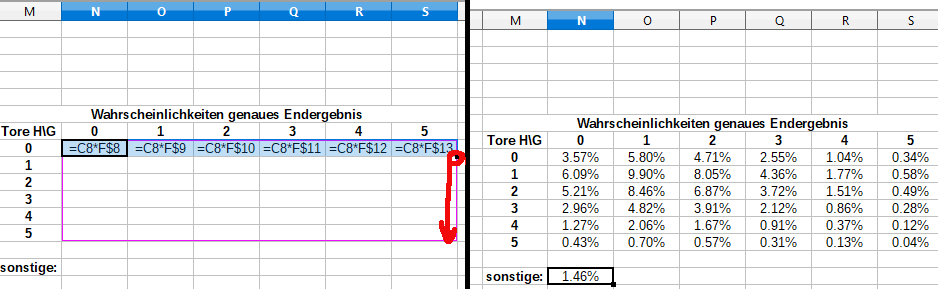
Tatsächlich kannst du mit Hilfe der Poisson-Verteilung auch die Wahrscheinlichkeiten für das genaue Ergebnis des Spiels berechnen. Erstelle dazu zunächst eine Ergebnismatrix nach folgendem Muster:
Um nun die Wahrscheinlichkeiten für die genauen Endergebnisse zu erhalten, multiplizierst du die exakten Wahrscheinlichkeiten für die entsprechende Anzahl von Toren je Team, die du in Schritt 2 berechnet hast. Um also beispielsweise auf die exakte Wahrscheinlichkeit eines 0-0 zu kommen, multiplizierst du die Wahrscheinlichkeit für 0 Tore für Eintracht Frankfurt (Zelle C8, 18.12%) mit der Wahrscheinlichkeit für 0 Tore für Bayer Leverkusen (Zelle F8, 19.69%). Dies wiederholst du für jede mögliche Kombination.
Gib folgende Formeln in die Zellen N8 bis S8 ein, damit du die restlichen Zeilen der Matrix durch Herunterziehen automatisch auffüllen kannst:
- N8: =C8*F$8
- O8: =C8*F$9
- P8: =C8*F$10
- Q8: =C8*F$11
- R8: =C8*F$12
- S8: =C8*F$13
Hier findest du den finalen Spreadsheet im .ods-Format:
| poisson.vert-naives-modell-sge-vs-b04-final.ods |
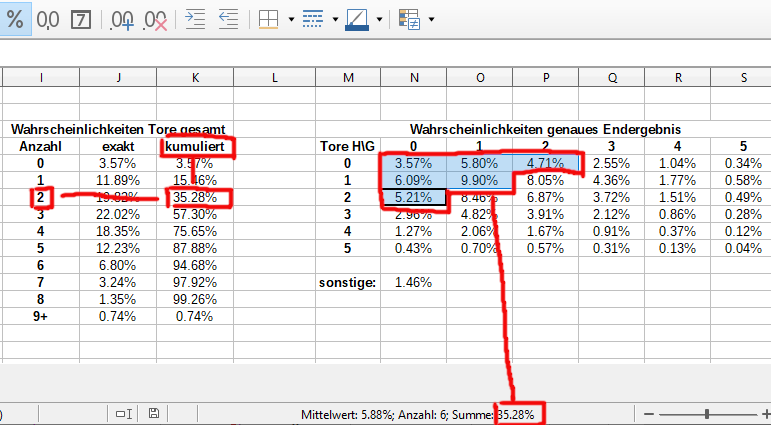
Wenn du alles richtig gemacht hast, dann sollten alle Ergebnisse in sich logisch stimmig sein. Wenn du beispielsweise in der Ergebnismatrix alle möglichen Spielstände für 2 Tore oder weniger markierst (also 0-0, 1-0, 2-0, 0-1, 1-1 und 0-2), dann sollte die in der Statusleiste angezeigte Summe dieser Wahrscheinlichkeiten exakt der Wahrscheinlichkeit für 2 Tore oder weniger in deiner Over/Under Tabelle in Zelle K10 entsprechen:
Schritt 5: Wahrscheinlichkeiten in Wettquoten umwandeln
Im letzten Schritt kannst du nun deine Wahrscheinlichkeiten mit Hilfe der 1/x-Formel in faire Wettquoten umwandeln. In manchen Fällen ist sehr offensichtlich, was zu tun ist (für Under 2.5 Tore beispielsweise nimmst du die Wahrscheinlichkeiten für 0, 1 und 2 Tore als Grundlage, für das Over die Gegenwahrscheinlichkeit). Für manche Optionen wird die Sache komplexer und würde hier den Rahmen sprengen, weshalb ich das Thema separat im nächsten Blogpost behandeln werde.
Die Schwächen der Poisson-Verteilung beim Sportwetten
Die Poisson-Verteilung ist ein nützliches Werkzeug für die Berechnung verschiedener Wahrscheinlichkeiten beim Wetten auf Sportereignisse, allerdings hat sie (wie jedes Modell) ihre Schwächen. Es ist wichtig, dass du dir dieser Schwächen bewusst bist, und die Poisson-Verteilung nicht blind anwendest.
1. Die Poisson-Verteilung beruht auf bestimmten Annahmen
Die Poisson-Verteilung beruht auf bestimmten Annahmen, die für ihre Verwendung mindestens näherungsweise gegeben sein müssen:
- Die Poisson-Verteilung muss Ereignisse beschreiben, deren Eintrittswahrscheinlichkeit relativ gering ist. Deshalb eignet sie sich vor allem für das Modellieren von Toren im Fußball oder Eishockey.
- Die Poisson-Verteilung nimmt an, dass alle beschriebenen Ereignisse unabhängig voneinander sind. Das ist bei Toren im Fußball nicht ganz der Fall, weil beispielsweise das Fallen des ersten Tores weitere Tore etwas wahrscheinlicher macht, und weil eine Führung in der Schlussphase aufgrund von Taktikänderungen ebenfalls eine etwas höhere Torwahrscheinlichkeit bewirkt. Der Effekt ist aber gering genug, um in aller Regel vernachlässigbar zu sein. Für Live-Szenarien kannst du diesem Effekt auch durch Anpassungen beikommen.
- Die Poisson-Verteilung nimmt an, dass der Zeitpunkt der Ereignisse zufällig ist, also das beispielsweise ein Tor in der ersten Halbzeit genauso wahrscheinlich ist wie in der zweiten Halbzeit. Das ist aufgrund der genannten Taktikeffekte aber nicht der Fall - du kannst im Fußball in so ziemlich jeder Liga beobachten, dass Tore in der zweiten Halbzeit etwas wahrscheinlicher sind. Solange du mit deinen Berechnungen und Wetten aber nur auf die Torrate des gesamten Spiels abzielst, ist dieser Aspekt irrelevant.
- Um für dein Sportwettenmodell gut zu funktionieren, darf dein Lamda (λ, der Torerwartungswert) nicht weit weg von der Varianz sein. Alles andere führt zu vermeidbaren Modellierungsfehlern.
Grundsätzlich hat jedes Modell und jeder Wettansatz seine blinden Flecken. Deshalb solltest du immer darauf bedacht sein, nach solchen systematischen Verzerrungen Ausschau zu halten und gegebenenfalls Korrekturen vornehmen.
2. Die Poisson-Verteilung beinhaltet keine Buchmachermarge
Die Poisson-Verteilung beinhaltet keine Buchmachermarge, sondern optimiert alle Wahrscheinlichkeiten auf 100%. Willst du sie zum Wetten verwenden, musst du erst noch selber einen Quotenpuffer einbauen, beispielsweise in dem du durch die Poisson-Verteilung ermittelte Wettquoten durch 1.05 oder ähnliche Faktoren teilst. Kommst du also zu einer Wahrscheinlichkeit von 50% (0.5), sähe deine Quotenberechnung mit Einbauen eines 1.05-Puffers (105% Overround) so aus:
3. Dein Output ist nur so gut wie dein Input
Auch für die Poisson-Verteilung gilt: Dein Output ist nur so gut wie dein Input. Wie zuverlässig deine so errechneten Wahrscheinlichkeiten sind, hängt sehr stark von der Qualität deiner Schätzung der Torerwartungswerte ab. Es ist nicht ideal, einfach nur den bisherigen Saisontorschnitt beider Mannschaften zu verrechnen, wie ich das weiter oben in den Beispielrechnungen getan habe. Ein besserer Ansatz ist beispielsweise das Heranziehen von Expected Goals (xG). Zu diesem Thema werde ich im übernächsten Teil der Wettmodellserie einen längeren Blogpost verfassen.
Fußnoten:
[1] Zu diesem Torerwartungswert kannst du auf sehr verschiedene Weisen kommen, und dieser Prozess macht einen sehr wesentlichen Teil deiner Modellierungsbemühungen aus. Das Schätzen dieses Wertes repräsentiert den Input, zu dem dir die Poisson-Verteilung einen sehr detailliert aufgeschlüsselten Output in Wahrscheinlichkeitsform gibt.
[2] Wenn wir annehmen, dass du den Torschnitt (dein Lambda λ) in Zelle A1 unterbringst, lautet die manuelle Formel für k = 2 Tore so: =((A1^2)/(FAKULTÄT(2)))*EXP(-A1)
Die 2 kannst du natürlich auch durch eine beliebige Zelle ersetzen.


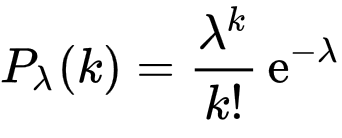
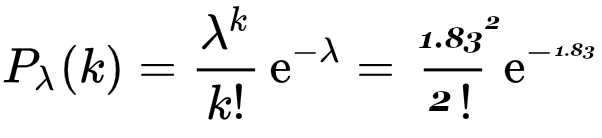



 RSS-Feed
RSS-Feed