Ich zeige dir, wie du die Poisson-Verteilung in Excel/Libre Calc verwendest, um mit Hilfe eines geschätzten Torerwartungswerts[1] für jedes Team Wahrscheinlichkeiten für jedes mögliche Ergebnis zu berechnen. In dieser Ausgabe lernst du, wie du mit Hilfe dieser Wahrscheinlichkeiten Wettquoten für das Over/Under berechnen kannst - auch in komplizierteren Fällen wie beispielsweise für Over/Under 2.75 Tore.
Im darauf folgenden Teil erkläre ich dir dann übernächste Woche, wie das für 1x2-Wetten und Asian Handicaps funktioniert.
Inhaltsverzeichnis
1. Was du für diesen Blogpost benötigst
Erweiterung des ursprünglichen Spreadsheets auf 8 Tore • Screenshots des erweiterten Grundlagen-Spreadsheets
2. Mit der Poisson-Verteilung Over/Under-Wettquoten berechnen: Grundlagen
Wie aus einer Wahrscheinlichkeit eine Wettquote entsteht
3. Berechnung der halben Over/Under-Wettquoten
4. Berechnung der ganzen Over/Under-Wettquoten
5. Berechnung der viertel Over/Under-Wettquoten
1. Was du für diesen Blogpost benötigst
Um das Berechnen der Wettquoten aus den Wahrscheinlichkeiten der Poisson-Verteilung zu meistern, wird dir insbesondere mein Blogpost zum Thema Wettquoten verstehen helfen.
Als Grundlage für alle Berechnungen dient mir dieser im vorangegangenen Blogpost zur Poisson-Verteilung erstellte Spreadsheet:
| poisson.vert-naives-modell-sge-vs-b04-final.ods |
Alle herunterladbaren Spreadsheets sind im .ods-Format gespeichert und können mit dem kostenlosen Libre Calc verwendet werden.
Erweiterung des ursprünglichen Spreadsheets auf 8 Tore
Ich habe diesen Spreadsheet ein wenig erweitert, um die Wettquoten detaillierter berechnen zu können. Die Logik bleibt exakt die selbe wie im vorangegangenen Poisson-Blogpost beschrieben, mit nur folgenden Unterschieden/Ergänzungen:
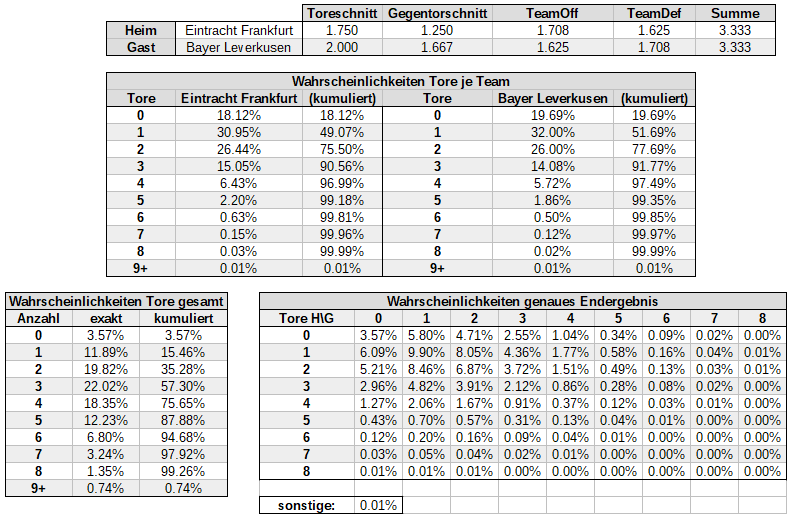
- Du siehst jetzt die einzelnen Wahrscheinlichkeiten für 0-8 Tore pro Team sowie die Wahrscheinlichkeit für 9 oder mehr Tore.
- Direkt daraus abgeleitet zeigt der Spreadsheet jetzt auch die Wahrscheinlichkeit für jedes exakte Endergebnis bis hin zu 8-8 an, sowie die Restwahrscheinlichkeit für jedes andere Endergebnis.
| poisson.vert-naives-modell-sge-vs-b04-erweitert-auf-8-tore.ods |
Screenshots des erweiterten Grundlagen-Spreadsheets
2. Mit der Poisson-Verteilung Over/Under-Wettquoten berechnen: Grundlagen
Beginnen wir zunächst mit der Berechnung der Over-Under Wettquoten, da das ein wenig einfacher zu organisieren ist. Zuvor lohnt sich noch ein kurzer Rückblick auf den Blogeintrag Wie berechnen sich Wettquoten?, insbesondere der Abschnitt “Wie du faire Wettquoten mit Brüchen berechnest”.
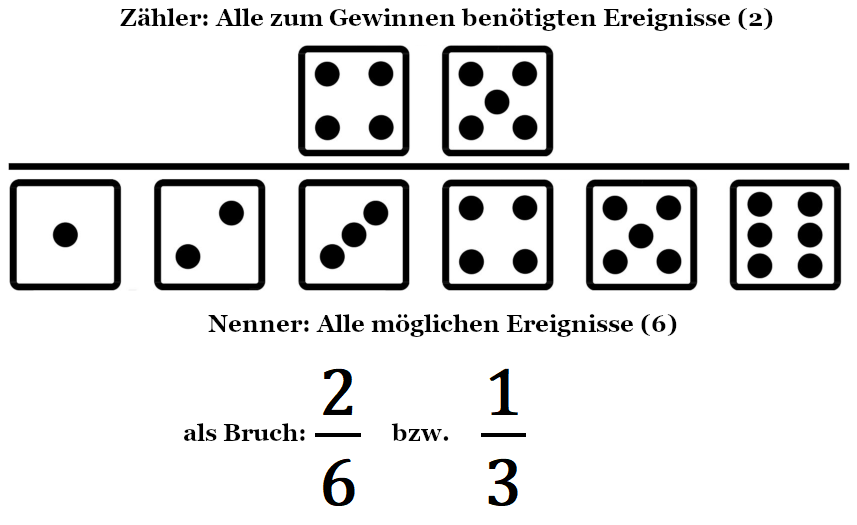
Wie eine Wahrscheinlichkeit als Bruch aussieht und wie daraus eine Wettquote entsteht
Die für jetzt wesentliche Erkenntnis aus dem Wettquoten-Blogpost ist, dass du eine Wahrscheinlichkeit (wie du sie zum Beispiel im Vorfeld mit der Poisson-Verteilung ausgerechnet hast) immer mit Brüchen ausdrücken kannst. Ein Bruch besteht immer aus zwei Komponenten, dem Zähler und dem Nenner. Für Wahrscheinlichkeiten gilt:
- Der Zähler besteht aus der Summe aller Eintrittswahrscheinlichkeiten - der Fälle also, in denen die Wette gewinnt.
- Der Nenner besteht aus der Summe der Wahrscheinlichkeiten aller theoretisch möglichen Ausgänge, in denen die Wette entweder gewinnt oder verliert[1].
Wenn du beispielsweise würfelst und entweder eine 4 oder eine 5 benötigst, dann kannst du deine Wahrscheinlichkeit, das erwünschte Ergebnis zu erhalten, ebenfalls als Bruch darstellen:
Um daraus eine Wettquote zu machen, nimmst du einfach den Kehrwert des Bruchs. Diese Operation entspricht exakt der dezimalen Inversion, die du auf dem Taschenrechner mit der 1/x-Taste bewerkstelligst.
Die selbe Inversion, einmal mit dem Kehrwert des Bruchs, und einmal dezimal mit dem Taschenrechner (1/x-Taste)
3. Berechnung der halben Over/Under-Wettquoten
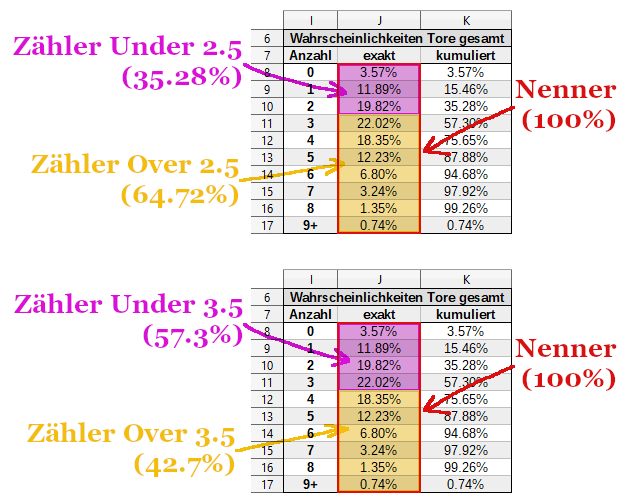
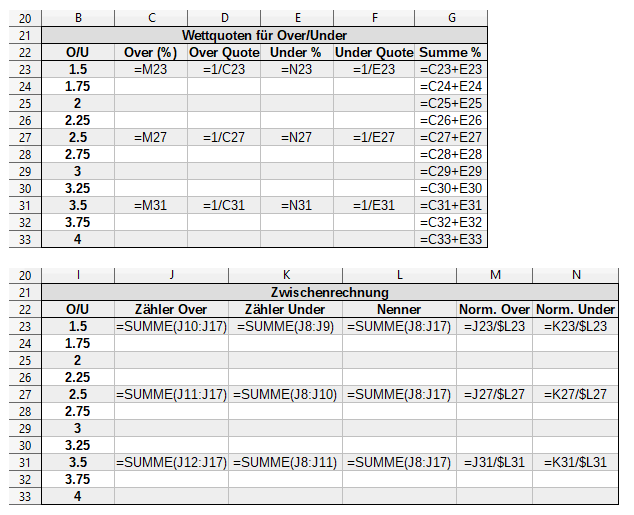
Am leichtesten ist die Berechnung der halben Over/Under-Wettquoten, wie zum Beispiel für Over/Under 2.5 Tore oder Over/Under 3.5 Tore. Der Grund dafür: Das Ereignis tritt entweder ein oder nicht; es gibt keine Grauzone, der Nenner liegt für halbe Over/Under-Wetten immer bei 100%. Für unsere Zwecke und mit unserem Spreadsheet als Beispiel kannst du also die notwendigen Brüche aus der Tabelle Wahrscheinlichkeiten Tore gesamt ableiten:
Wie Nenner und Zähler für die Wahrscheinlichkeiten von Over/Under 2.5 Toren und O/U 3.5 Toren aussehen
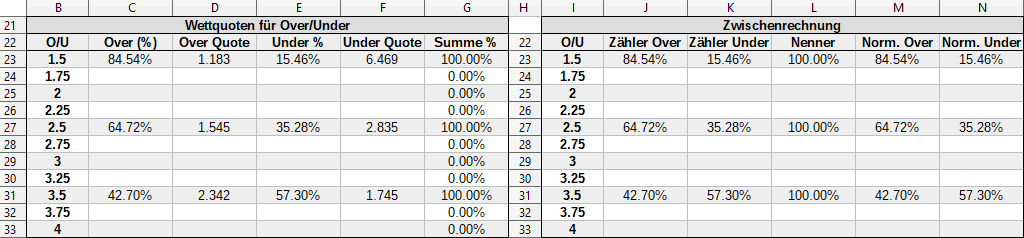
Das kannst du folgendermaßen in einen Spreadsheet gießen:
Die Wahrscheinlichkeiten, die sich für die halben Over/Under-Wettquoten ergeben.
Hier eine downloadbare Version des Spreadsheets, nachdem alle obigen Schritte vollzogen sind:
| poisson.vert-naives-modell-sge-vs-b04-halbe-over-under-komplett.ods |
4. Berechnung der ganzen Over/Under-Wettquoten
Für ganze Over/Under-Wettquoten ist die Lage ein wenig komplizierter, weil die jeweils in der Linie enthaltene Toranzahl (bei Over/Under 3 also jedes Ergebnis mit genau 3 Toren) dazu führt, dass die Wette null und nichtig ist, und du den Einsatz zurück erhältst. Um die Wettquote korrekt darzustellen, musst du deshalb die Wahrscheinlichkeit für die betreffende Anzahl an Toren im Spiel weglassen. Und zwar gilt das für den Nenner genauso wie den Zähler.
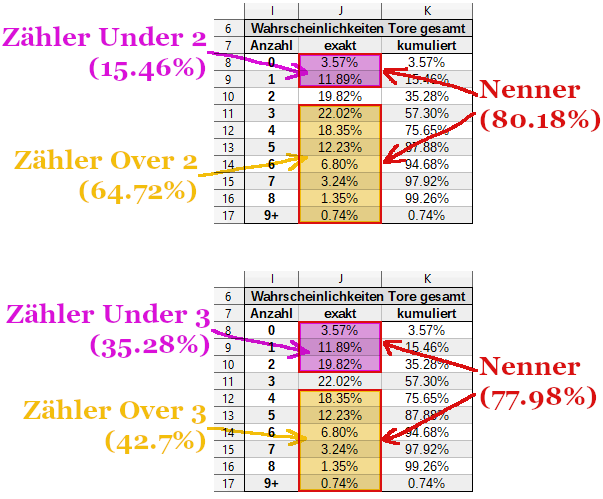
Das kannst du dir schematisch so vorstellen:
Das führt dazu, dass du nicht mehr wie vorher noch eine saubere 100% im Nenner stehen hast, sondern stattdessen eine niedrigere, krumme Prozentzahl. Was auch logisch ist, da von den 100% schließlich die Wahrscheinlichkeit abgezogen werden muss, die der exakten Toranzahl der betreffenden O/U-Linie entspricht.
Das bedeutet auch, dass du die Wahrscheinlichkeiten im Zähler erst einmal normalisieren musst. Das erreichst du, indem du sowohl den Over- als auch den Under-Zähler durch den Nenner teilst. So landest du bei den korrekten Wahrscheinlichkeiten, die du dann einfach durch Inversion (1/x) zu einer Wettquote umwandelst.
Markiert die Ergebnisse der neu eingefügten Berechnungen für die ganzen Over/Under-Linien
Erneut die selben beiden Tabellen, diesmal auf Formelebene. Die oben im Text geschilderte Normalisierung geschieht in den Spalten M und N. Auf den korrekten Nenner kommst du, in dem du von den 100% (J8:J17) die Wahrscheinlichkeit der entsprechenden exakten Toranzahl abziehst (-J10/-J11/-J12).
Und so sieht der gesamte Spreadsheet nach dem Einfügen der ganzen Over/Under-Linien aus:
| poisson.vert-naives-modell-sge-vs-b04-ganze-over-under-komplett.ods |
5. Berechnung der viertel Over/Under-Wettquoten
Noch ein wenig schwieriger wird es, wenn es an viertel Over/Under-Linien wie O/U 2.75 oder O/U 3.25 geht. Hier lauert die größte Falle: Nicht wenige denken beispielsweise, dass man für die Over 3.25 Linie einfach nur den Schnitt der Wettquoten von Over 3 und Over 3.5 nehmen muss, oder wahlweise den Schnitt der zugrunde liegenden Wahrscheinlichkeiten. Das ist aber nicht richtig. Zu korrekten Wettquoten gelangst du nur, wenn du den oben beschrittenen Weg mit Zähler und Nenner gehst.
Das Schema funktioniert so ähnlich wie bei den ganzen Over/Under-Wettquoten. Das ergibt Sinn, denn eine viertel Over/Under Linie wird schließlich zur Hälfte aus einer ganzen Over/Under-Linie gebildet.
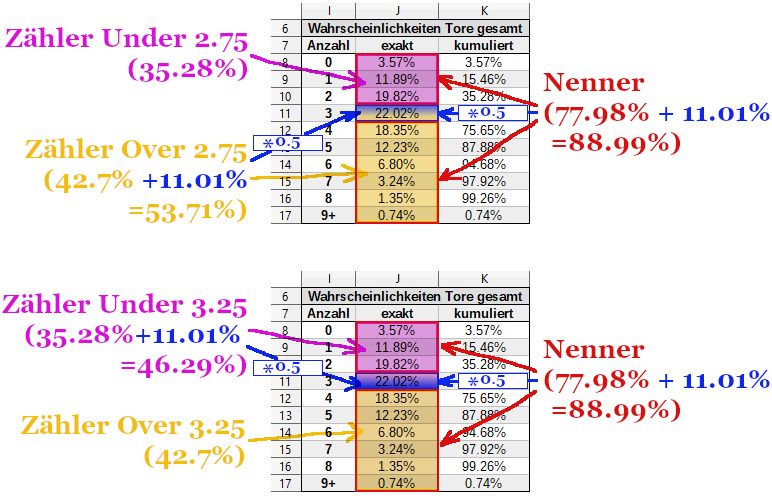
Der wichtige Unterschied ist folgender: Statt die Wahrscheinlichkeit der exakten Toranzahl ganz wegzulassen, berücksichtigst du sie zur Hälfte. Im Schema unten beispielsweise beträgt die Wahrscheinlichkeit für exakt drei Tore 22.02%, also lässt du 11.01% in den Nenner einfließen. Ferner fließt diese Hälfte zudem noch in den Zähler der Wette, die bei der entsprechenden Toranzahl halb gewinnen würde. Bei exakt drei Toren gewinnt jeweils das Over 2.75 und das Under 3.25 halb; entsprechend baust du die 11.01% in diese Zähler ein, nicht aber ihre Gegenstücke. So sieht das im Schema aus:
Die etwas kompliziertere Bildung von Zähler und Nenner für viertel Over/Under-Linien: Für exakt drei Tore fließt die halbe Wahrscheinlichkeit in den Nenner und den Zähler der halb gewinnenden Wette.
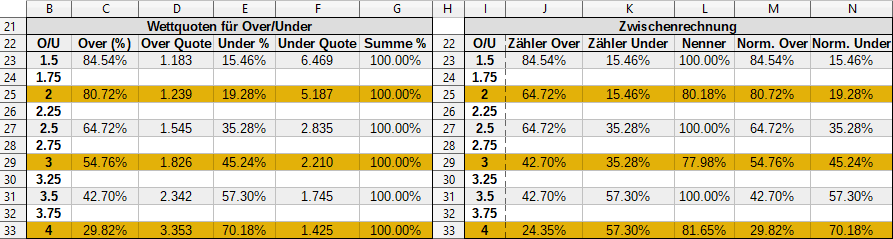
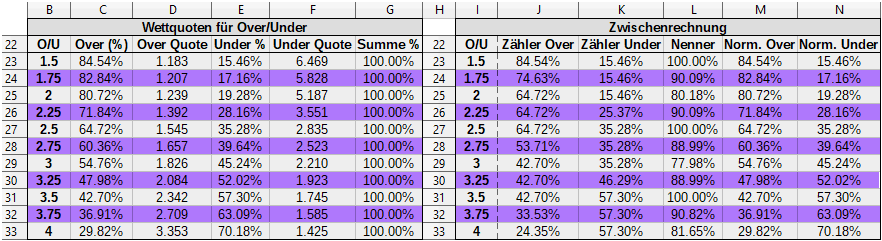
Im Spreadsheet sieht das mit den korrekten Formeln im Ergebnis so aus:
Markiert die ergänzten viertel Over/Under-Linien
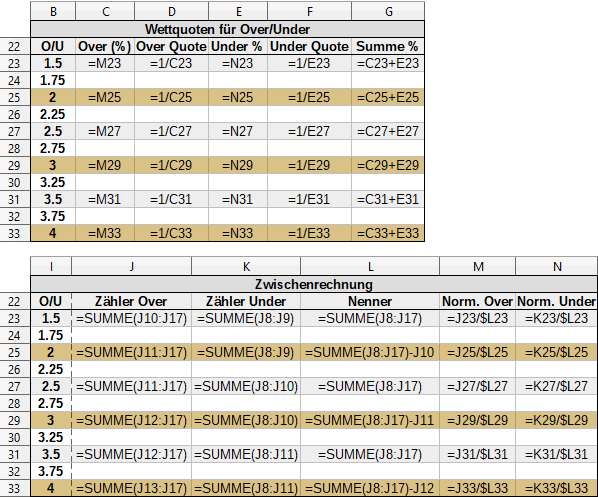
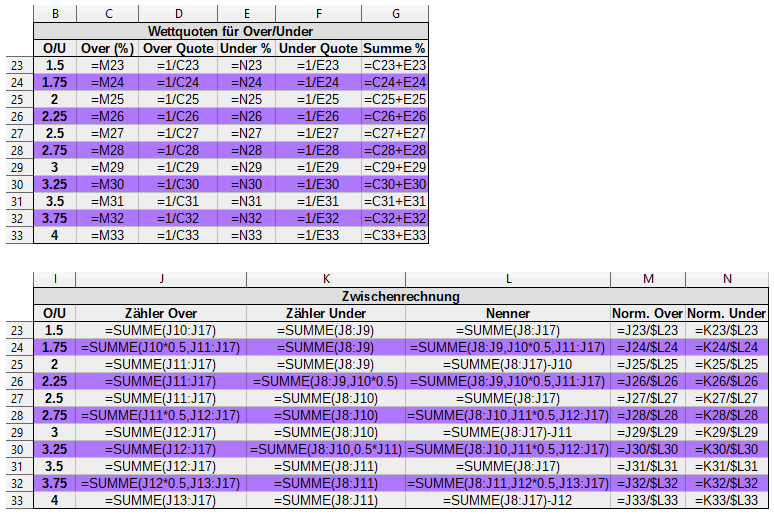
Und so sieht alles auf Formelebene aus:
Hier noch einmal der jetzt komplette Spreadsheet:
| poisson.vert-naives-modell-sge-vs-b04-viertel-over-under-komplett.ods |
Im nächsten Teil der Wettmodellserie geht es darum, wie der gleichen Prozess für Asian Handicap-Wettquoten und 1x2-Quoten aussieht.
Fußnoten:
[1] Es ist wichtig zu verstehen, dass die mit Hilfe der Poisson-Verteilung berechneten Wahrscheinlichkeiten immer nur so gut sein können, wie die ihnen zugrunde liegende Schätzung der Torerwartungswerte für jedes Team. Wenn diese Schätzungen falsch sind, wirkt sich das naturgemäß auf alle anderen Werte aus.
[2] Wie du im Abschnitt zur Berechnung von ganzen Over/Under-Wettquoten erfährst: Die Wahrscheinlichkeiten der Spielergebnisse, die zu einem Push führen (Geld zurück), werden weder im Nenner, noch im Zähler berücksichtigt. Weil es in diesen Fällen so ist, als habe es keine Wette gegeben.
RSS-Feed