Mit dieser Formel rechnest du Wettquoten in Wahrscheinlichkeiten um
Mit dem Taschenrechner Wahrscheinlichkeiten aus deinen Wettquoten berechnen
Sollte auf deinem Taschenrechner keine 1/x-Taste vorhanden sein, teile einfach 1 durch die Wettquote. Verfügst du über diese Taste, gib die Wettquote ein und drücke dann 1/x:
Und so sieht die Rechnung auf Formelebene aus:
Beispiel: Umwandlung der Wettquote 2.50 in ihre Wahrscheinlichkeit
Das funktioniert auf diese Weise mit jeder beliebigen Wettquote, nehmen wir als Beispiel die Wettquote 2.50:
Die Rechnung auf Formelebene:
Du kannst umgekehrt auch Wahrscheinlichkeiten in Wettquoten umwandeln
Diese Rechnung funktioniert auch umgekehrt. Wenn du Wahrscheinlichkeiten in Wettquoten umwandeln möchtest, dann tust du das auf dem Taschenrechner mit der selben Taste. Als Formel sieht das dann folgendermaßen aus:
Berechnen wir also als Beispiel die Wettquote, die zur Wahrscheinlichkeit 40% gehört:
Auf dem Taschenrechner:
Wettquoten verstehen: Ein visueller Ansatz
Wenn du dir neben Dezimalquoten im Wettquoten-Vergleich noch andere Formate anschaust, wie zum Beispiel fraktionale Wettquoten, dann wird klarer, dass sie alle auf einer einfachen Logik aufbauen – und diese nur jeweils anders ausdrücken. Es geht immer darum, deinen Wetteinsatz im Verhältnis zu dem deiner Gegenpartei zu sehen.
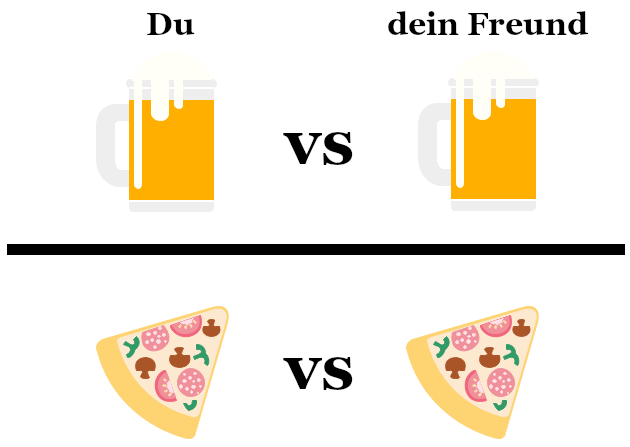
Sicher hast du schon einmal mit Freunden um ein Abendessen oder ein Bier gewettet.
Um an dieser Wette teilzunehmen, riskierst du also den selben Einsatz wie dein Freund. Lass uns daraus deine eigene Wettquote berechnen:
Das sieht erst einmal sehr einfach aus, und dennoch kannst du aus diesem Diagramm eine Menge ableiten:
- Ihr setzt beide ein Bier, das Verhältnis eurer Wetten liegt also bei 1:1. Dieser Wert entspricht zugleich auch der fraktionalen Quote dieser Wette, 1/1.
- Beide Einsätze aufaddiert ergeben ein Gesamtvolumen von 2.
- Du kannst sowohl deinen Einsatz, als auch den Einsatz deines Freundes in Beziehung zum Gesamtvolumen der Wette setzen und das als ½ ausdrücken, oder 0.5 als Dezimalzahl. Das entspricht den 50% des Gesamteinsatzes, die ihr jeweils haltet.
- Das Gesamtvolumen von 2 entspricht zugleich auch der Dezimalquote dieser Wette, 2.00.
Bei Dezimalquoten wird dein Einsatz immer durch eine 1 repräsentiert, was deutlicher wird, wenn wir dieses Diagramm für eine Wette mit einem Buchmacher zu einer Quote von 3.00 zeichnen:
Schematische Darstellung einer Wette mit Quote 3.00
- Du setzt einen Säckchen Geld, der Buchmacher die doppelte Menge. Das Verhältnis eurer möglichen Gewinne liegt also aus deiner Sicht bei 2:1 (du kannst zwei Einheiten gewinnen und riskierst dafür eine), was auch exakt der fraktionalen Schreibweise 2/1 entspricht.
- Dein Einsatz (1) und der des Buchmachers (2) ergeben aufaddiert ein Gesamtvolumen von 3
- Erneut kannst du deinen Einsatz (1) zum Gesamtvolumen (3) ins Verhältnis setzen, und landest damit bei ⅓, also 0.33 bzw. 33%.
- Das Gesamtvolumen von 3 dieser Wette entspricht aus deiner Sicht der Dezimalquote dieser Wette (3.00).
Die Quote berechnen - und die Gegenquote
Der letzte Punkt ist wichtig, um Wettquoten wirklich zu verstehen: Der Buchmacher erhält für seine Wette nicht die Quote 3.00, sondern die Gegenquote dazu. Bei fraktionalen Quoten musst für die Gegenquote einfach nur die Einsätze drehen: Beträgt die fraktionale Quote aus deiner Sicht 2/1, dann wird für den Buchmacher daraus automatisch eine 1/2.
Bei Dezimalquoten ist die Lage allerdings anders: Weil in einer Dezimalquote der Einsatz immer als 1 eingepreist ist, musst du die Einsatzverteilung ein wenig umformen.
- dein Einsatz: 1, Buchmachereinsatz: 2
- teile beide Einsätze durch 2
- du erhältst: 0.5 Einsatz für dich, 1 für den Buchmacher.
So sieht das in der Grafik für den Buchmacher aus:
Schematische Darstellung einer Wettquote von 1.50
- Der Buchmacher riskiert in diesem Schema eine Einheit, und du nur eine halbe. Fraktional wäre diese Darstellung unschön, weshalb man dort auf ganze Einheiten verdoppelt.
- Der Einsatz des Buchmachers (1) und deiner (0.5) ergeben aufaddiert ein Gesamtvolumen von 1.5
- Wenn du den Einsatz des Buchmachers ins Verhältnis zum Gesamtvolumen setzt, ergibt das 1/1.5, oder anders ausgedrückt ⅔, bzw. 0.66 = 66%
- Das Gesamtvolumen von 1.5 entspricht der Dezimalquote dieser Wette (1.50) aus Sicht des Buchmachers.
Die dezimale Gegenquote zu 3.00 ist also 1.50.
Wie du Wahrscheinlichkeiten im Verhältnis zu Wettquoten verstehen kannst
In den obigen schematischen Diagrammen habe ich davon geschrieben, dass du deinen Einsatz ins Verhältnis zum Gesamtvolumen setzen kannst. Das ist ein sehr wichtiges Konzept. Nehmen wir zunächst ein weiteres Beispiel:
Schematische Darstellung einer Wette mit Dezimalquote 4.00
- Du setzt eine Einheit, der Buchmacher drei, daher lautet deine fraktionale Quote 3/1 (und die fraktionale Gegenquote des Buchmachers 1/3)
- Dein Einsatz (1) und der Einsatz des Buchmachers (3) ergeben aufaddiert ein Gesamtvolumen von 4
- Das Gesamtvolumen von 4 sagt bedeutet, dass deine Dezimalquote für diese Wette bei 4.00 liegt
- Du kannst deinen Einsatz (1) ins Verhältnis zum Gesamtvolumen (4) setzen, und landest damit bei ¼, also 0.25 bzw. 25%.
- Du kannst auch den Einsatz des Buchmachers (3) ins Verhältnis zum Gesamtvolumen (4) setzen, und landest damit bei ¾, also 0.75 bzw. 75%. (woraus du ableiten kannst, dass die dezimale Gegenquote 1 / 0.75 ≈ 1.33 lautet)
Wettquoten und ihre implizierten Wahrscheinlichkeiten
Die beiden zuletzt genannten Prozentzahlen (25% für die Wettquote 4.00, 75% für deren dezimale Gegenquote 1.33) nennt man auch die implizierten Wahrscheinlichkeiten der zugehörigen Wettquoten. Wettquoten sind also nur eine andere Möglichkeit, Wahrscheinlichkeiten auszudrücken.
Wenn du für eine beliebige Wettquote die zugehörige implizierte Wahrscheinlichkeit berechnest, ermittelst du im Kern, in wie viel Prozent der Fälle du deine Wette gewinnen musst, um keine Verluste zu machen. Wenn du also zu einer Quote von 2.00 wettest, musst du dafür 50% deiner Wetten gewinnen, bei einer 4.00 sind es 25% deiner Wetten, usw.
In gewisser Weise berechnest du so also den Nullpunkt deiner Wette. Gewinnst du häufiger, landest du in der Profitzone, gewinnst du seltener, landest du in der Verlustzone. Diesen Nullpunkt einer Wettquote bezeichnet man auch als faire Quote, da du mit dieser Wettquote (im Mittel) weder Gewinne noch Verlust machen würdest.
Wettquoten als Wahrscheinlichkeiten: 100% - 50%
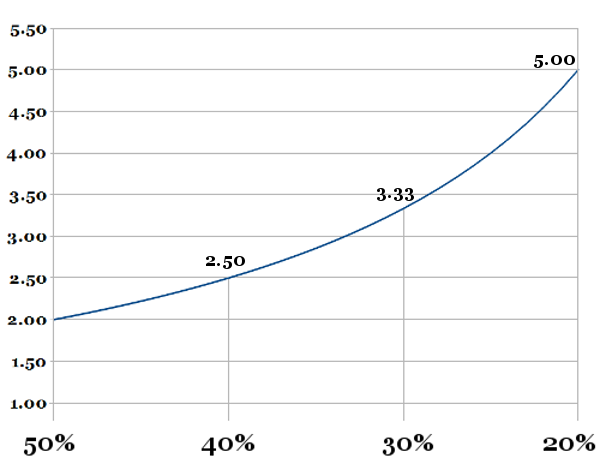
Wettquoten als Wahrscheinlichkeiten: 50% - 20%
Vor- und Nachteile von Dezimalquoten
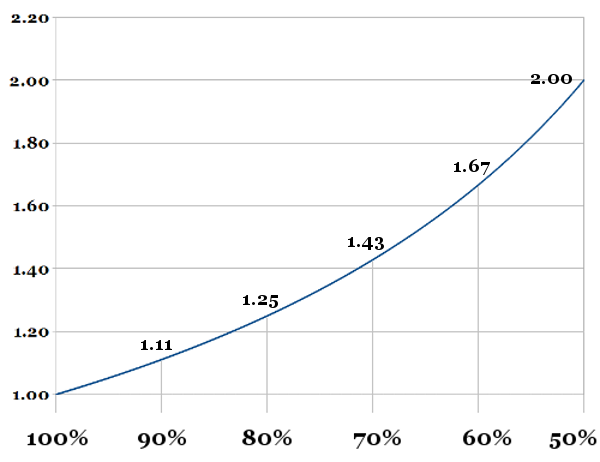
Es gibt bei Dezimalquoten einen exponentiellen Zusammenhang zu ihren implizierten Wahrscheinlichkeiten, Dezimalquoten sind ideal, wenn du sie in Wahrscheinlichkeiten umrechnen möchtest und umgekehrt; sie sind aber nicht dafür geeignet, intuitiv Abstände zwischen Wettquoten verstehen zu können.
Das liegt daran, dass der Bereich von 100% bis 50% im Dezimalquotenbereich von 1.00 bis 2.00 erfasst wird, während der Bereich unterhalb von 50% mit Quoten oberhalb von 2.00 beschrieben wird.
Andere Wettquotenformate
Es gibt auch eine Reihe anderer Wettquotenformate, die sich dafür besser eignen, weil sie wie das hier beschriebene fraktionale System oder auch wie das amerikanische System Quote und Gegenquote spiegeln. Dazu, und zu den Vor- und Nachteilen der einzelnen Systeme, in einem zukünftigen Blogpost mehr.

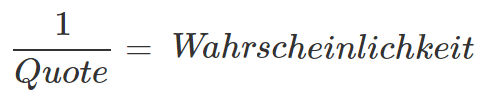

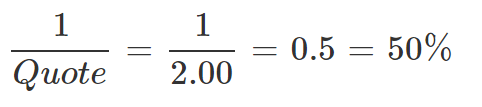

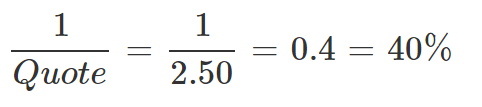
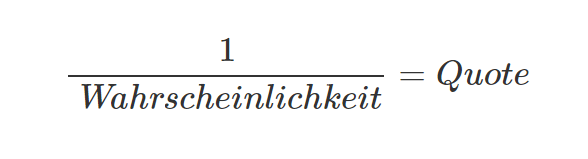
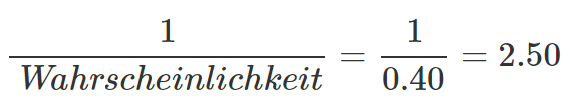





 RSS-Feed
RSS-Feed