Zufallsindikatoren (3): Quotienten errechnen

30/7/2016

Wenn du die im Rahmen dieses Blogs bereits vorgestellten Zufallsindikatoren WTB (Wett-Tabelle), OTV+1 und OTV-S verwendest, ergibt sich ein Problem: Die Werte sind nicht direkt vergleichbar. Das kannst du mit einem einfachen Kniff beheben: Indem du die Standardabweichung berechnest, und die Werte durch diese teilst. Um dies aber wirklich gründlich tun zu können, sollten wir zunächst einen Schritt zurück gehen: Auf die Spieltagspaarungen.

Letztendlich ist der relevanteste Wert der Wett-Tabelle und der anderen Zufallsindikatoren nicht der absolute Wert jedes Teams, sondern die Differenz der beiden Teams, die sich am nächsten Spieltag gegenüber stehen. Wenn wir beispielsweise den nächsten (17.) Spieltag der brasilianischen Serie A anschauen, ergeben sich für die anstehenden Paarungen folgende Differenzen für die drei Zufallsindikatoren (aus Sicht des Heimteams):

Die Zufallsindikatoren für die Partien des 17. Spieltags (aus Heimsicht)

#	Heim	Gast
1	Figueirense	Vitoria
2	Sport Recife	Atletico PR
3	Atletico MG	Santa Cruz
4	Fluminense	Ponte Preta
5	Sao Paulo	Chapecoense AF
6	Coritiba	Flamengo
7	Internacional	Corinthians
8	Santos FC	Cruzeiro
9	America MG	Gremio
10	Botafogo RJ	Palmeiras

Im nächsten Schritt musst du nun die Standardabweichung berechnen^[1]. Ein beliebter Fehler ist an dieser Stelle, lediglich die vorhandenen Paarungen zu berücksichtigen. Es ist allerdings wichtig, im Hinterkopf zu behalten, dass die Spieltagspaarungen nur einen Bruchteil der möglichen Begegnungen repräsentieren – für die Standardabweichung sind gleichermaßen diejenigen Begegnungen von Bedeutung, die nicht stattfinden, aber theoretisch möglich wären.

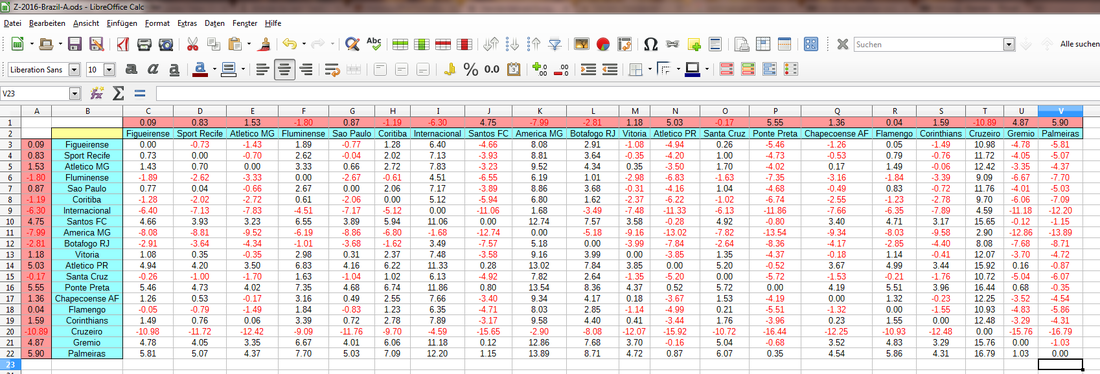
Zu diesem Zweck musst du in deinem Spreadsheet eine Matrix erstellen, die die Differenzen aller theoretisch möglichen Paarungen abbildet. Wie das funktioniert, zeige ich dir am folgenden Beispiel:

Eine Begegnungs-Matrix für alle Teams erstellen (am Beispiel der Wett-Tabelle)

Um die Matrix zu erstellen, empfiehlt sich ein neues Tabellenblatt in deinem Spreadsheet. In diesem Beispiel habe ich Zelle B2 (gelb) dafür vorgesehen, die Standardabweichung für die Matrix anzuzeigen. In die Zellen B3 bis B22 (hellblau) kommen die Namen der 20 Ligateams; in die Zellen A3 bis A22 die WTB-Werte der betreffenden Teams.

Schritt 1: Die Teams einfügen

Am leichtesten ist es zu diesem Zweck, copy and paste zu verwenden. Kleiner Trick: Um das Übernehmen von Formatierungen zu vermeiden, klicke nach dem Kopieren der gewünschten Inhalte mit rechts auf den Einfügebereich und wähle die Option Inhalte einfügen. Darauf folgt eine Dialogbox mit verschiedenen Optionen, auf die ich weiter unten aufgehe – momentan musst du einfach nur bestätigen.

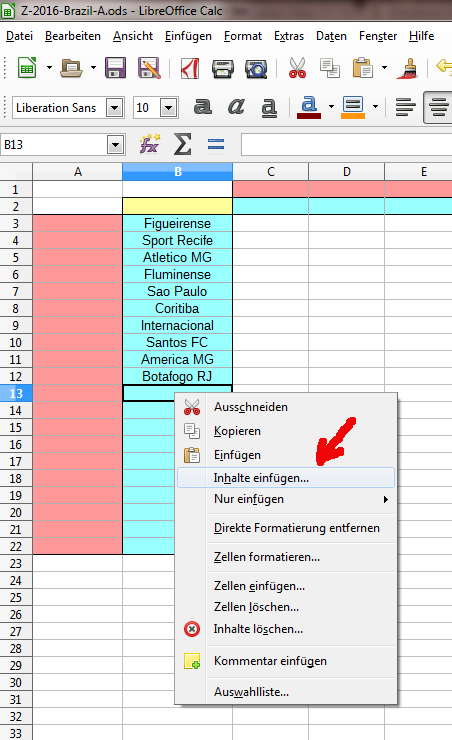
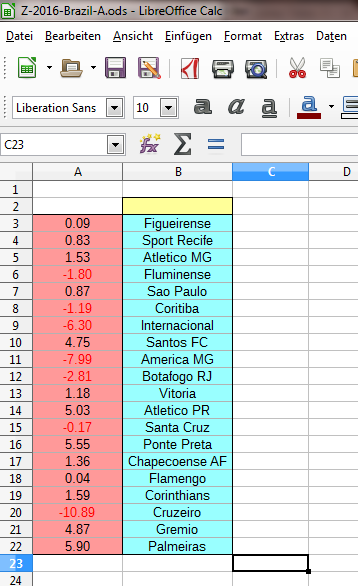
Schritt 2: Die Teamwerte einfügen

Nach dem gleichen Muster überträgst du jetzt die passenden Teamwerte, in diesem Beispiel die Werte der Wett-Tabelle:

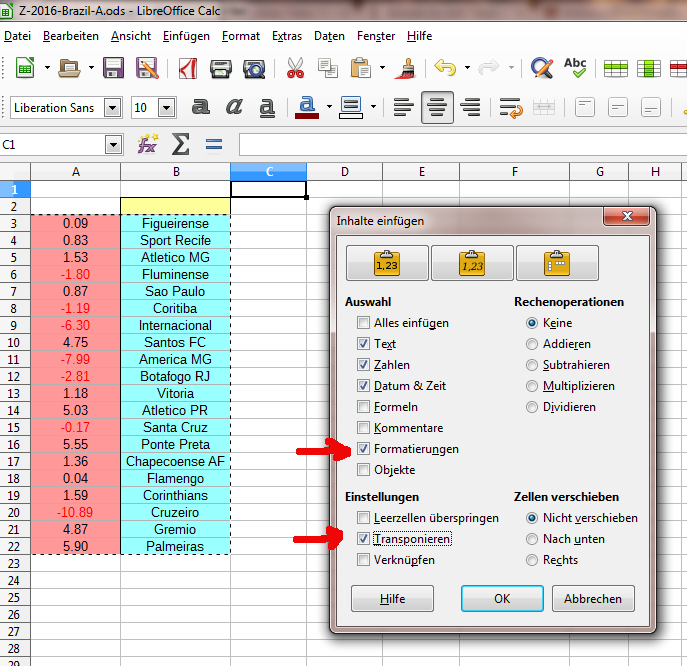
Schritt 3: Kopfzeile erstellen

Um nun eine Matrix zu erstellen, benötigst du eine identische Kopfzeile mit Teamnamen und -werten. Dazu kopierst du zunächst die Inhalte der Zellen A3 bis B22 (markieren und Strg+C drücken). Klicke dann mit rechts auf Zelle C1, wähle Inhalte einfügen, und markiere in der folgenden Dialogbox die Punkte Formatierungen (um die Formatierungen beizubehalten, wie die Anzahl der Nachkommastellen und die Hintergrundfarbe) sowie den Punkt Transponieren.

Transponieren bewirkt, dass die Werte aus den Spalten A und B nicht vertikal eingefügt werden, sondern horizontal. Das Ergebnis sieht dann folgendermaßen aus:

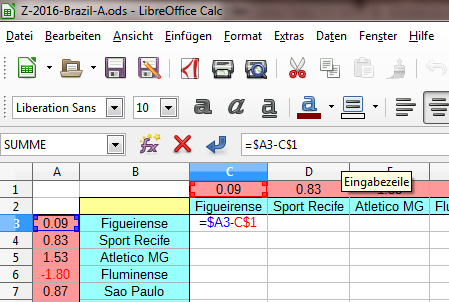
Schritt 4: Grundbaustein der Matrix

Gib nun in Zelle C3 die folgende Formel ein:

=$A3-C$1

Das Ergebnis für Zelle C3 selber lautet nun notwendigerweise 0, da hier der Wert von Figueirense mit sich selbst verglichen wird. Das muss überall dort in der Matrix der Fall sein, wo ein Team auf sich selber trifft. Das erste Dollarzeichen dient dazu, beim automatischen Auffüllen der Spalten D bis V den Buchstaben A konstant zu halten; entsprechend hält das zweite Dollarzeichen die Zahl 1 konstant, sobald du danach die Zeilen 4 bis 22 automatisch auffüllst.

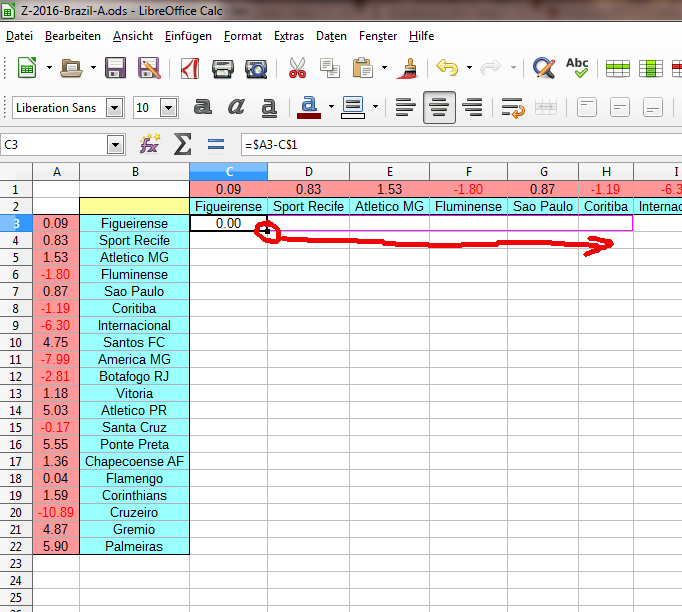
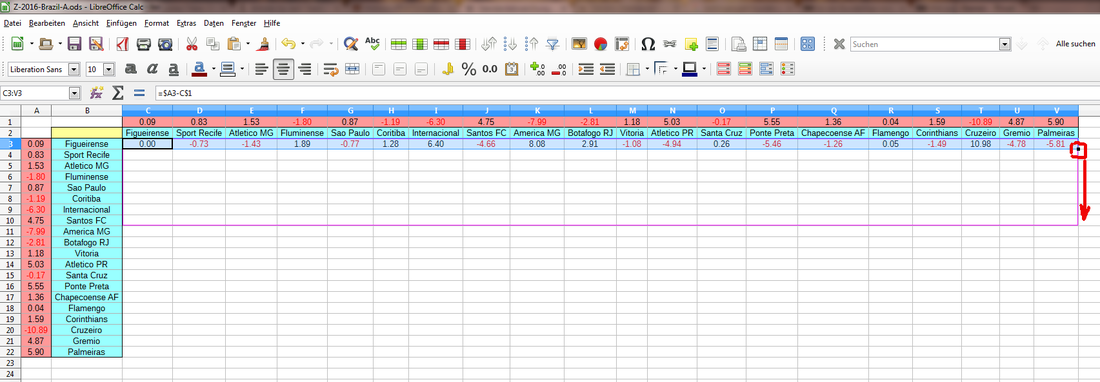
Schritt 5: Die Spalten der Matrix auffüllen

Um die Spalten der Matrix aufzufüllen, ziehe das kleine schwarze Quadrat in Zelle C3 bis Spalte V hinüber.

Schritt 6: Die Zeilen der Matrix auffüllen

Markiere jetzt die Zellen C3 bis V3, und ziehe das kleine schwarze Quadrat bis Zeile 22 hinunter. Alternativ kannst du es auch doppelt anklicken.

Die Matrix sollte jetzt so aussehen:

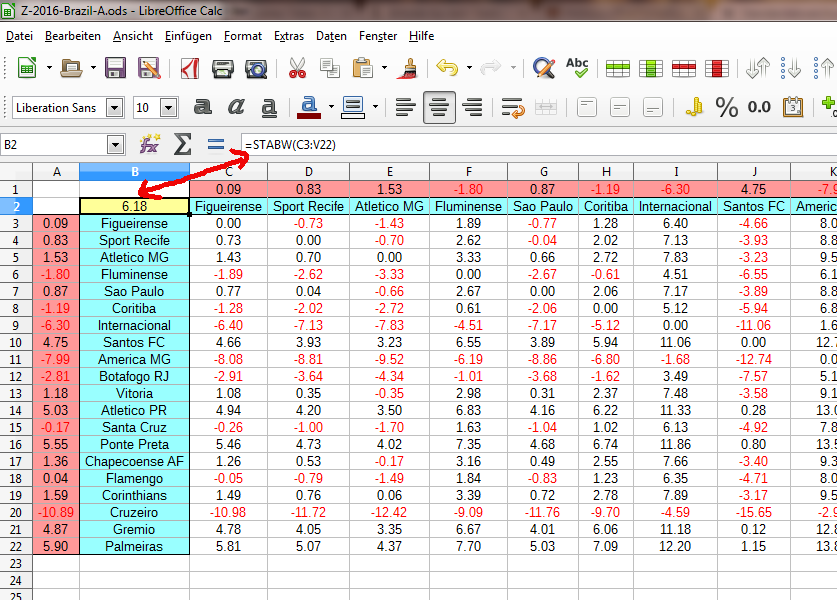
Schritt 7: Standardabweichung der Matrix berechnen

Um die Standardabweichung der Matrix zu berechnen, verwendest du in Zelle B2 diese Formel:

=STABW(C3:V22)

Die so berechnete Standardabweichung verwendest du nun, um zu sehen, wie extrem die Zufallswerte der kommenden Partien relativ zu allen möglichen Ligabegegnungen ausfallen.

Das erreichst du (wie eingangs erwähnt), indem du die Differenz der entsprechenden Partie durch die Standardabweichung teilst.

Die Quotienten für die Paarungen des 17. Spieltags (aus Sicht der Heimteams)

Wenn du diese Schritte für alle Zufallsindikatoren nachvollziehst, ergeben sich für den aktuellen Spieltag folgende Quotienten:

#	Heim	Gast
1	Figueirense	Vitoria
2	Sport Recife	Atletico PR
3	Atletico MG	Santa Cruz
4	Fluminense	Ponte Preta
5	Sao Paulo	Chapecoense AF
6	Coritiba	Flamengo
7	Internacional	Corinthians
8	Santos FC	Cruzeiro
9	America MG	Gremio
10	Botafogo RJ	Palmeiras

Während der weitere Umgang mit diesen Indikatoren weiterhin Interpretationssache bleibt (wie das beim Fällen von Wettentscheidungen letztlich immer der Fall ist), hast du mit dem Ermitteln der Quotienten nun aber eine Möglichkeit, die relative Seltenheit der beobachteten Werte besser vergleichen zu können.

Interessant wird es insbesondere bei Werten oberhalb von +1 bzw unterhalb von -1. Größer als +1 bedeutet, dass das Heimteam in der entsprechenden Kategorie ordentlich Glück hatte verglichen mit dem Auswärtsteam, und das Umgekehrte gilt bei kleiner als -1.

Beim Blick auf die Paarungen des 17. Spieltags fällt also zum Beispiel auf, dass Ponte Preta recht viel Glück in allen Kategorien hatte verglichen mit Fluminense.

Das legt eine Wette auf Fluminense nahe, da das Team vermutlich eher unterbewertet werden wird vom Markt.

Fußnoten:

¹ Die Standardabweichung berechnet sich aus der Quadratwurzel der Varianz. Diese berechnet sich aus dem quadrierten Abstand aller Werte zum Tabellenschnitt.

31 Comments

Dennis

30/7/2016 18:47:29

Und die Quotienten der Standartabweichung beeinflussen deine Wettentscheidung inwiefern?
(Ist nicht so leicht zu verstehen für Nicht-Statistiker) :)

Crimson Corporation link

30/7/2016 21:06:03

@Dennis - tut mir leid, hätte ich genauer erklären können. Die Quotienten auszurechnen ermöglicht es zunächst einmal, WTB, OTV-S und OTV+1 direkt zu vergleichen.

Ansonsten wird es insbesondere bei Werten oberhalb von +1 bzw unterhalb von -1 interessant. Größer als +1 bedeutet, dass das Heimteam in der entsprechenden Kategorie ordentlich Glück hatte verglichen mit dem Auswärtsteam, und das Umgekehrte gilt bei kleiner als -1.

Beim Blick auf die Paarungen des 17. Spieltags fällt also zum Beispiel auf, dass Ponte Preta recht viel Glück in allen Kategorien hatte verglichen mit Fluminense.

Das legt eine Wette auf Fluminense nahe, da das Team vermutlich eher unterbewertet werden wird vom Markt. (aber natürlich sollte das nicht die einzige Entscheidungsgrundlage sein, aber es ist schon ein klarer Wink)

Dennis

31/7/2016 06:02:42

Sehr schön. Das habe ich verstanden. :)

Was ich leider immer noch nicht verstanden habe ist OTV-S. Bin mir aber auch nicht zu schade um nochmal zu fragen :D

Nehmen wir als Beispiel das Spiel gestern aus der Serie A Figueirense vs Vitoria.

Figueirense: Schüsse aufs Tor: 3
Vitoria: Schüsse aufs Tor: 2

Figueirense: Schüsse neben das Tor: 1
Vitoria: Schüsse neben das Tor: 6

Figueirense gesamt: 4
Vitoria gesamt: 8

Gewicht A: 4/(4+8) = 0.333

SQ Figueirense: 0.3*0.667+0.1*0.333 = 0.166

SQ Vitoria:0.2*0.667+0.6*0.333 = 0.333

Und was mache ich jetzt ?

Gruß & Sorry,

Dennis

Christopher

30/7/2016 22:24:44

Grüß dich Joachim,

Ist die Standardabweichung für jede Art von Erwartungswerten von Variablen besser geeignet beim vergleichen als dieses klassische 30% zu 70% Vergleichsmuster und hat es den wichtigen Vorteil mit dem Vergleich von negativen und positiven Zahlen?

Ich habe dir vor einiger Zeit eine mathematische Frage gestellt, zum Thema ''Vergleich von 2 Mittelwerten. Kann es sein, dass du nur mit der Standardabweichung in deinen Wettmodellen arbeitest?

Hier ist der Link noch mal

http://www.crimsoncorporation.de/wettblog/wett-tabelle-der-bundesliga-201516-22-spieltag

1. Bundesliga 2013/2014 Medianwerte ExpG und Gegner ExpG

Verein ExpG Gegner ExpG
Gladbach 0,25 -0,50
Hoffenheim 0,45 0,55
Leverkusen 0,60 -0,10
Bayern 0,50 -0,25
Dortmund 0,60 0,00
Hamburg -0,10 0,45
Wolfsburg 0,30 0,10
Mainz 0,15 -0,20
Schalke 0,25 -0,15
Freiburg 0,05 0,15
Hannover -0,10 0,40
Stuttgart -0,20 0,30
Augsburg -0,15 0,20
Bremen 0,00 0,20
Hertha 0,10 0,35
Frankfurt -0,15 0,10
Nürnberg 0,05
Braunschweig-0,50

So gehen wir einmal davon aus, man würde die Korrelation von diesen Erwartungswerten berechnen, welche Methode hätte den höheren Korrelationskoeffizienten?

Die Standardabweichungsmethode oder dieser klassische Vergleich mit den 70% zu 30%, basierend auf der Frage vom Februar?

Crimson Corporation link

7/8/2016 08:50:55

Ja, ist besser geeignet.

Daytrader

2/8/2016 17:53:01

Super hilfreich. Vielen Dank dafür. :)

Was kann man(n) den in den nächsten Wochen hier noch so erwarten ?

Singbet

3/8/2016 11:35:44

Sollten alle 3 Werte (WTB, OTV & OTS) über +1/-1 sein damit eine Wette für dich in Frage kommt ?

Crimson Corporation link

7/8/2016 08:47:35

Nicht zwingend. Wenn die Summe der Werte ca. +2/-2 übertrifft, dann ist das zum Beispiel auch ganz gut.

Letztlich immer eine Ermessensfrage, und natürlich auch kontextabhängig.

Singbet

7/8/2016 21:33:13

Wobei wahrscheinlich OTV-S & WTB stärker zu gewichten sind als OTV +1 oder ?

Daytrader

3/8/2016 15:50:32

Ist es realistisch wenn ein Agent zu mir sagt er bekommt 0.25% vom Umsatz des Buchmachers ? Er bietet mir an die 0.25% zu teilen, 50/50 !?

Was meinst du ?

Crimson Corporation link

7/8/2016 08:41:07

@Daytrader

Ja, das klingt realistisch. Letztlich aber auch nicht der entscheidende Punkt, wichtiger ist, dass man sich auf einander verlassen kann - profitabel wetten musst du so oder so.

Zwecks Risikostreuung (sowohl was das Kapital, aber auch die Information anbelangt) empfiehlt es sich aber ohnehin, mehr als nur einen Agenten zu verwenden. Und dann siehst du ja, was dir andere in dieser Hinsicht anbieten.

Daytrader

3/8/2016 15:55:51

http://www.bilder-upload.eu/show.php?file=433103-1470232723.jpg

Christopher

6/8/2016 10:49:31

Joachim, wenn du irgendwann einen Blogpost zum Thema Taylor Model schreiben solltest, möchte ich dich darauf hinweisen, dass ich noch einmal die Maße genauer abgemessen habe, ohne Pixelruler, sondern mit einem Lineal.

Statt der 164, nur noch die 163.
Umrechnungszahl ist 0,0672
Elfmeter Wahrscheinlichkeit ist 72,5%

Das sind nun meine finalen Spreadsheet Werte, und ich bin absolut begeistert von den Ergebnissen.

Die Methodik mit der Standardabweichung habe inzwischen verstanden.

Mich würde es auch einmal interessieren, was man in absehbarer Zeit besonders in der Fußball Wett Theorie noch erwarten kann.

Das aufwendige Taylor Model für Fußball ist für mich ein Indiz, dass ein Wissenvorsprung nur durch harte Arbeit erlangt werden kann und das gilt auch für andere Sportarten.

Was US Sport anbelangt interessiere ich mich besonders für Baseball und Basketball. Einfach nur die Statistiken aus bestimmten Statistik Seiten abzukopieren reicht bestimmt noch lange nicht, um den Wettmarkt zu schlagen.

Crimson Corporation link

10/8/2016 17:50:13

Vielen Dank für den Hinweis.

Semih

6/8/2016 13:21:30

@Christoph

Die Ergebnisse stimmen? aber weißt du, ob du auch Value spielst?

Christopher

6/8/2016 14:18:11

Die Closing Line wird sehr oft geschlagen, weil der Wettmarkt zum Beispiel nur die geschossenen Tore zählen wird und wir haben durch das Taylor Model einen Vorteil.

Ich weiß gar nicht genau, in welcher Wettart den Wettprofis am meisten gelingt, den Wettmarkt zu schlagen, weil man andere Sportwetter beobachtet, kann man feststellen, dass manche auch bis kurz vor der Closing Line warten, bis sie wetten werden.

Man bekommt sozusagen ein Gespür für die Quotenbewegungen der Wettmärkte.

Ich bin gerade dabei, meine Quoten mit den Pinnacle Quoten zu vergleichen, und man hat dadurch immer einen Vorteil gegenüber den Freizeit Wettern, welche nur die geschossenen Tore oder die vielleicht auch noch die Torschussrate als Indikator nehmen werden.

Überlege einmal, wenn Mannschaft A und Mannschaft B, 3 mal hintereinander nur 0 Tore schießen in ihren Begegnungen, werden viele Amateure und Freizeitspieler 3 Mal die 0 zählen als Erwartungswert mit ihren Poisson Rechner.

Und was ist passiert? 7 Tore sind auf einmal gefallen. Darum sollte man mit Erwartungswerten arbeiten, weil es genauere Ergebnisse liefert wird.

So habe ich das damals auch am Anfang gemacht und habe mich gewundert, warum ich keine Gewinne gemacht habe.

Darum ist die Korrelation mit Taylor am höchsten im Vergleich zu den anderen Methoden.

Wenn du verunsichert bist, dann überprüfe die Maße doch selbst einmal und du wirst festellen, dass du ungefähr die selben Werte bekommen wirst.

Semih

6/8/2016 15:57:37

Ja, ich weiß dass es das genauste Modell zurzeit ist, dennoch muss ich ja nah an die Eröffnungsquoten kommen, ist dies auch der Fall?

Und noch so eine Frage am rande, mit welchem System arbeitest du mit deinem Rechner, Windows 10?

Christopher

6/8/2016 18:42:21

Windows 8

So jetzt werde ich einmal erklären wie ich auf diese Werte komme, damit auch jeder das nachvollziehen kann.

Elfmeter Wayne Rooney

http://www.fourfourtwo.com/statszone/8-2015/matches/803368/team-stats/1/0_SHOT_09#tabs-wrapper-anchor#:utyjnhWSTDy8wA

Die Breite der Grafik beträgt 529 Pixel.
Gemessen wird ab der gestrichelten Linie.
14,95 cm von oben nach unten gemessen.
4,6 cm von oben bis zur Torauslinie.
4,6 cm von 14,95 = 30,77%
30,77% von 529 = 162.7733 ~ 163

y1 341,55 (X Koordinate)
x1 380 (Y Koordinate)

341,55 - 163 = 178,55
12 / 178,55 = 0,0672

Ich möchte noch den Hinweis geben, dass die Elfmeter Koordinaten auch mal ein wenig abweichen können von diesen beiden Werten.

Zum Thema Closing Line kann ich im Moment nur folgendes sagen, dass ich schon einige Spiele beobachtet habe, wo meine Quote war z.B bei 2,06 und die Opening Odds war so um die 2,32 und die Closing Line war so um die 2,15 gewesen. Wie bereits erwähnt, habe ich schon mehrere Spiele beobachtet, wo man die Closing Line geschlagen hätte. Bedenke bitte, dass die Quoten bei der Closing Line am effektivsten sind. Bei den Asian Handicaps ist das nicht immer der Fall.

Was ich im Moment noch überprüfen müsste und werde, was diese Over/Under Wetten anbelangt, was denn genau als ausreichende Anzahl von vergangenen Spielen man in Betracht ziehen müsste um auch möglichst nicht zu starke Diskrepanzen zwischen meiner Quote und der Buchmacher zu riskieren. Die Erwartungswerte können auch schwanken, da ist es vielleicht sinnvoll, längere Zeitspannen, wie z.b. die ganze aktuelle Saison, und nicht nur die letzten 5 Spiele in Betracht zu ziehen.

Christopher

6/8/2016 20:03:50

''Seit dem ich mich auf diese Zufallsbasierten Ansätze konzentriere, sind die Resultate gut. Aber da ich jetzt in den meißten Fällen nur noch gegen den Markt gehe schlage ich kaum noch die Closing Line ? Wird sich das auf lange Sicht negativ bemerkbar machen? ''

''Die Closing Line zu schlagen ist letztlich auch nur ein Indikator, kein Selbstzweck - solange die Ergebnisse passen, würde ich mir darüber an deiner Stelle nicht zu viele Gedanken machen.''

Diesen Hinweis sollte man unbedingt berücksichtigen, weil wenn man mit diesen Erwartungswerten arbeitet, müsste die Closing Line eine nicht mehr so starke Rolle spielen, denn was zählt ist das man nach mehreren tausend Wetten im Plus landet, als wenn man ständig nur noch die Pinnacle Closing Line im Auge behalten müsste, nach dem Motto ich habe die Closing Line nicht geschlagen, also müsste die Wette nicht value gewesen sein.

Semih

6/8/2016 21:25:25

Ja da hat Joachim auch recht, zumal muss man auch gucken, wie er schon sagte, wo man seine Wette spielt - in Brasilien ist der Markt nicht so effizient.

Aber die Eröffnungssquoten sind schon wichtig. Ich glaube auch, dass expG ein gutes Modell ist, aber es bringt mir ja auch nur was, so lange ich Value spiele.

Okay ich muss auch mal gucken - ob ich mir ein anderes Windows zulege - der Visual Web Ripper hat nicht funktioniert. Womöglich hab ich auch die Möglichkeit mir den Content Grabber zu holen.

Crimson Corporation link

7/8/2016 09:11:57

@ Dennis 31/7/2016 05:02:42

Erst berechnest du das relative Gewicht der Schusswerte: Schüsse Team A / (Schüsse A + Schüsse B) und dito für Team B. (

Dann betrachtest du Spielausgang, wobei gilt: Sieg 1, Unentschieden 0.5, Niederlage 0.

Das relative Schussgewicht ziehst du vom Spielausgang ab.

Ergibt für dein Beispiel folgende Rechnung:

SQ Figueirense: 0.166 / (0.166 + 0.333) = 0.333

SQ Vitoria: 0.333 / (0.166 + 0.333) = 0.667

Figueirense hat gewonnen, ergo ergibt sich 1 - 0.333 = +0.667

Vitoria hat verloren, also: 0 - 0.667 = -0.667

Manuel

1/2/2018 09:02:56

Hallo,

was für einen Sinn macht den im Nachgang eine Berechnung ob Gewonnen oder verloren?

Ich kann doch die Formel auch im laufenden Spiel anwenden, wie Spieltag z.b 24 wo es z.b Siege:4 gab und Niederlagen:20 ?

Aber leider ergibt die Rechnung keinen Sinn:
4 - 0,333 = 3,667

Habt ihr da ein Tipp?

Christopher

7/8/2016 09:36:29

Ich habe noch mal mehrere Spiele mit diesen Taylor Model Ansatz überprüft und bin im Moment etwas enttäuscht, weil es hat den Anschein, als ob das nicht für Over/Under Wetten geeignet ist, weil zu oft liegen zwischen meiner Quote und der Buchmacher Quote zu große Abstände.

Es scheint so, als ob dieser Ansatz besonders nur für Asian Handicap zu gebrauchen ist.

Ich werde aber noch mal einen anderen Ansatz überprüfen, die ExpG eines Teams und immer des Gegners mit addieren und das als Richtwert zu nehmen, wie ich das sonst bei den Over/Under Wetten immer genutzt habe. Vielleicht gibt es dann bessere.Ergebnisse.

Christopher

7/8/2016 14:45:43

Heureka, ich hüpfe im Quadrat vor freude. :)

Ich denke, wenn man die Erwartungswerte auf und abrundet, bekommt man bessere Ergebnisse, weil die Korrelation ist sehr aussagekräftig finde ich. Ich schätze in etwa, dass langfristig in etwa 50% der Fälle die Tore einer Mannschaft korrekt sein werden, die so berechnet werden.

Beispiel 1. FC Köln 2014/2015

1 Spieltag Köln - Hamburg 0-0 ExpG Köln 0,4 ~ 0
2. Spieltag Stuttgart - Kön 0-2 ExpG Köln 1,6 ~ 2
3. Spieltag Paderborn - Köln 0-0 ExpG Köln 0,3 ~ 0
4. Spieltag Köln - Gladbach 0-0 ExpG Köln 0,3 ~ 0
5. Spieltag Hannover - Köln 1-0 ExpG Köln 0,7 ~ 1
6. Spieltag Köln - Bayern 0-2 ExpG Köln 1 ~ 1
7. Spieltag Frankfurt - Köln 3-2 ExpG Köln 0,5 ~ 1
8. Spieltag Köln - Dortmund 2-1 ExpG Köln 0,7 ~ 1
9. Spieltag Bremen - Köln 0-1 ExpG Köln 0,8 ~ 1
10. Spieltag Köln - Freiburg 0-1 ExpG Köln 1,1 ~ 1
11. Spieltag Hoffenheim - Köln 3-4 ExpG Köln 0,7 ~ 1
12. Spieltag Köln - Hertha 1-2 ExpG Köln 1,4 ~ 1
13. Spieltag Leverkusen - Köln 5-1 ExpG Köln 0,9 ~ 1
14. Spieltag Köln - Augsburg 1-2 ExpG Köln 1,3 ~ 1
15. Spieltag Schalke - Köln 1-2 ExpG Köln 1 ~ 1
16. Spieltag Köln - Mainz 0-0 ExpG Köln 1,1 ~ 1
17. Spieltag Wolfsburg - Köln 2-1 ExpG Köln 0,6 ~ 1
18. Spieltag Hamburg - Köln 0-2 ExpG Köln 2,2 ~ 2
19. Spieltag Köln - Stuttgart 0-0 ExpG Köln 0,5 ~ 1
20. Spieltag Köln - Paderborn 0-0 ExpG Köln 1 ~ 1
21. Spieltag Gladbach - Köln 1-0 ExpG Köln 0,5 ~ 1
22. Spieltag Köln - Hannover 1-1 ExpG Köln 1,2 ~ 1
23. Spieltag Bayern - Köln 4-1 ExpG Köln 0,8 ~ 1
24. Spieltag Köln - Frankfurt 4-2 ExpG Köln 0,7 ~ 1
25. Spieltag Dortmund - Köln 0-0 ExpG Köln 0,5 ~ 1
26. Spieltag Köln - Bremen 1-1 ExpG Köln 2 ~ 2
27. Spieltag Freiburg - Köln 1-0 ExpG Köln 1 ~ 1
28. Spieltag Köln - Hoffenheim 3-2 ExpG Köln 3 ~ 3
29. Spieltag Hertha - Köln 0-0 ExpG Köln 0,6 ~ 1
30. Spieltag Köln - Leverkusen 1-1 ExpG Köln 1,7 ~ 2
31. Spieltag Augsburg - Köln 0-0 ExpG Köln 0,3 ~ 0
32. Spieltag Köln - Schalke 2-0 ExpG Köln 1,4 ~ 1
33. Spieltag Mainz - Köln 2-0 ExpG Köln 0,8 ~ 1
34. Spieltag Köln - Wolfsburg 2-2 ExpG Köln 1,7 ~ 2

15 von 34 richtig

Singbet

8/8/2016 12:10:55

Nochmal ne Frage zu Elo:

Wie würdest du es handhaben bei einem Derby mit dem Heimvorteil ? Einfach so lassen oder reduzieren ?

Crimson Corporation link

10/8/2016 17:46:48

Am Besten ist es, wenn du dein Eloratings um den Heimvorteil bereinigst (also das "pure" Elo-Rating berechnest) und dann vor dem Spiel entsprechend anpasst für Heim- und Auswärtsmannschaft.

Daytrader

8/8/2016 12:57:06

Hast du zufällig Erfahrungen mit Mollybet? Falls ja, wie sind die ?

Crimson Corporation link

10/8/2016 17:41:37

Ja, habe ich. Früher gab es häufiger mal Probleme zu Stoßzeiten, hauptsächlich wenn die ganzen englischen Spiele samstags um 16 Uhr live gehen, aber das ist jetzt auch schon 2-3 Jahre her.

Funktioniert sehr zuverlässig und ist ideal, wenn du bei mehreren Bookies gleichzeitig Wetten willst. Lohnt sich aber vermutlich auch nur, wenn du das regelmäßig tust, weil du entsprechende Summen setzt.

Crimson Corporation link

10/8/2016 17:44:44

Re: Was es zu erwarten gibt in den nächsten Wochen:

Ich will einen Blogpost schreiben, um die Elo/Spreadsheet-Geschichte um eine elegante Funktion zu erweitern, die Sache mit dem Baseballmodell steht aus, und evt. stelle ich einen weiteren Zufallsindikator vor. Ferner will ich mich auch mal wieder den Themen Riskomanagement und Wettpsychologie widmen.

Christopher

14/8/2016 13:04:45

Hallo Joachim,

ich möchte einmal deinen Rat hören, was du von Regressionsanalysen denkst und ob du selbst diese Methode anwendest. Ich weiß nicht so recht, ob das nur ein Proxy oder ob es sich dabei, um ein absolutes Muss in einem Wettmodell sich darstellen könnte, besonders wenn man mit Erwartungswerten über längere Zeiträume arbeitet.

Stimmt diese These, dass viele Statistiken von Webseiten für die Katz sind? Baseball Reference, Basketball Reference, American Football Reference z.B., dass es sich leider nur um Mainstream Daten handelt, welche die meisten Sportwetter eben nutzen werden? Man muss halt einen anderen Weg gehen, um wichtige Informationen zu erlangen, die der Wettmarkt nicht haben wird? Beispiel im Fußball - Taylor Model. ExpG Statistiken existieren auf keiner Statistik Seite. Der Hintergrund liegt einfach darin, dass das Wettmodel von einem Profi von einem Amateur sich dadurch unterscheidet, dass der Wettprofi mehr Informationen berücksichtigt, wie die Tore zählenden Amateure.

...und ich habe damals für solche Tore zählenden Wett Amateur Autoren auch noch Geld dafür bezahlt. Das ist Jahre her. Solche Sprüche wie ich wette bei Betfair, und lebe von Sportwetten, machen einem natürlich neugierig seinen Horizont zu erweitern. Die Erkenntnis hatte ich erst später feststellen können. Ein 1500€ Bankroll Lehrmeister :) und auf 1,15-1,20 Quoten wettender Sportwetter kann nie und nimmer nur von Sportwetten leben und wenn man glaubt, dass man mit simplen Torgezähle Strategien langfristig Gewinne machen könnte, genau das war damals der Grund gewesen, warum ich mir eine Auszeit genommen habe, weil ich genug hatte, von diesen Halbwissen Sportwettern aus Deutschland, wo ich einiges an Lehrgeld dafür bezahlt hatte, damit meine ich, dass diese Strategien nicht wirksam waren.

Zum Thema US Sport:

Hattest du jemals einen Lehrer, was das US Sportwetten anbelangt, der dich zu deinem heutigen Wissen geführt hat, oder musstest du Jahrelang das Internet durchforsten, um irgendwelche Anhaltspunkte zu bekommen, was denn genau eine Mannschaft gewinnen oder verlieren lässt?

Um ehrlich zu sein Joachim, fühle ich mich, was das US Sport anbelangt, dass ich dort eher noch im Dunkeln tappen muss und auch werde, weil man eben versuchen sollte, wertvolle Erwartungswerte zu kreieren, welche der Wettmarkt nicht haben wird, und der Wettprofi kann dadurch seinen entscheidenden Vorteil gewährleisten.

Es hat den Anschein, als ob diese Beiträge von US Universitäten mit Fachgebieten der Mathematik und Statistik einen sagen wir mal, einen kleinen Blick erlauben, welche Statistiken sinnvoll sein könnten, bloß ich habe kein Vertrauen in diese Statistik Seiten, weil ich lebe mehr nach dem Motto, ''Traue keiner Statistik, welche du nicht selbst gefälscht hast.''

Ein Kritiker, wird am besten dadurch überzeugt, in dem er sein eigenes Evidenzmoment hat. Und seitdem ich deine Beiträge bei Bettingexpert vor zirka einem halbem Jahr gelesen habe, wusste ich sofort, dass du absolut überzeugt bist, von dem was du schreibst, besonders was das Thema Wetttheorie belangt.

Christopher

24/8/2016 04:25:33

Zu dem Thema Quotienten berechnen habe ich noch ein paar Gedanken im Moment zusammen gefasst und ein Beispiel genommen von der 1. Bundesliga Saison 2014/2015 vor dem 7. Spieltag.

Aus Sicht der Heimmannschaft

# Heim Gast WTB OTV+1 Taylor ExpG
1 Hertha Stuttgart -0,24 -0,54 1,63
2 Bayern Hannover -1,07 -0,08 -0,16
3 Dortmund Hamburg -0,44 2,68 1,44
4 Leverkusen Paderborn -0,64 0,58 0,10
5 Hoffenheim Schalke 0,30 0,00 -0,62
6 Bremen Freiburg -0,14 -0,22 1,11
7 Frankfurt Köln 0,83 0,74 1,11
8 Wolfsburg Augsburg -0,63 -0,34 0,49
9 Gladbach Mainz 0,01 0,45 -1,01

Dient diese Standardabweichungsmethode mit dazu zum Modulieren der fairen Quote?

Sind in Wettmärkten mit weniger Volumen tatsächlich weniger Value Quoten zu beobachten?

Zum Thema Psychologie im Wetten mein Vorschlag dazu, wäre das Thema Mindset.

Was meinst du mit diesen Hinweis mit dem Elo Rating mit dieser eleganteren Funktion? Könntest du vielleicht im Moment das schon konkreter beschreiben?

Ein Thema was mich im Moment bewegt, weil ich im Moment ein automatisiertes Spieler Elo Rating erstelle, wo ich nur das Elo Rating +/- und die Spieldauer des Spielers eingeben muss, wäre das Thema ''Welche Spieler wird der Trainer im nächsten Spiel aufstellen?''

Du hast in einem deiner Posts bei Bettingexpert das erwähnt mit einem Modell der Mannschaftsaufstellungen und ich finde das sehr interessant. 1-2 Stunden vor dem Spiel, wenn der Trainer die Aufstellungen bekannt geben wird durch Twitter und sonst wo, ist der Value meist eh schon weg. Daher sollte man schon ein paar Tage eher wetten, weil am Matchtag ist massiv mit Wettprofi Quoten Bewegungen zu rechnen. Bloß woher soll man wissen, welche Spieler der Trainer in 3-4 Tagen aufstellen wird?

Richtig Wetten.

Zufallsindikatoren (3): Quotienten errechnen

Die Zufallsindikatoren für die Partien des 17. Spieltags (aus Heimsicht)

Eine Begegnungs-Matrix für alle Teams erstellen (am Beispiel der Wett-Tabelle)

Schritt 1: Die Teams einfügen

Schritt 2: Die Teamwerte einfügen

Schritt 3: Kopfzeile erstellen

Schritt 4: Grundbaustein der Matrix

Schritt 5: Die Spalten der Matrix auffüllen

Schritt 6: Die Zeilen der Matrix auffüllen

Schritt 7: Standardabweichung der Matrix berechnen

Die Quotienten für die Paarungen des 17. Spieltags (aus Sicht der Heimteams)

Fußnoten:

Leave a Reply.

Autor