Was ist eine optimale Torverteilung?
In seltenen Ereignissen steckt viel Zufall
Allerdings steckt in Toren meist ein ordentlicher Schuss Zufall. Das gilt gleich auf zwei Ebenen:
- Tore hängen oft von zahlreichen kleinen Zufällen ab: Schiedsrichterentscheidungen, Wetterbedingungen, abgefälschte Schüsse, etc.
- Tore sind seltene Ereignisse, die sich zufällig häufen können
Optimale Torverteilungen hängen mit dem letzten Punkt zusammen. So ziemlich jeder Fußballfan hat das schon live erlebt: Der eigene Club dominiert den Gegner und erspielt sich Chance um Chance; dennoch steht am Ende nur ein Unentschieden, oder gar eine Niederlage. Reporter faseln in solchen Momenten gerne etwas von der Cleverness oder Effizienz des Gegners, in aller Regel ist die Ursache aber im Zufall zu suchen.
Torschüsse haben nur eine relativ geringe Chance, verwandelt zu werden. Aus diesem Grund kann es für ein Team zufallsbedingt sehr leicht zu längeren Torflauten oder Phasen mit wenigen Toren kommen, sowohl innerhalb eines Spiels, als auch über mehrere Spiele hinweg. Und auf der anderen Seite des Medaillen kommt es immer wieder zu Phasen, in denen man einen Lauf hat 1.
Knappe Spiele sind zufallsanfällig
Generell gilt das natürlich auch für Unentschieden, allerdings ist in diesen Fällen nicht automatisch klar, wer hier mehr Glück gehabt haben könnte. Dazu in einem künftigen Blogpost dieser Reihe mehr. Konzentrieren wir uns hier also ausschließlich auf Spiele, die mit nur einem Tor Unterschied gewonnen wurden.
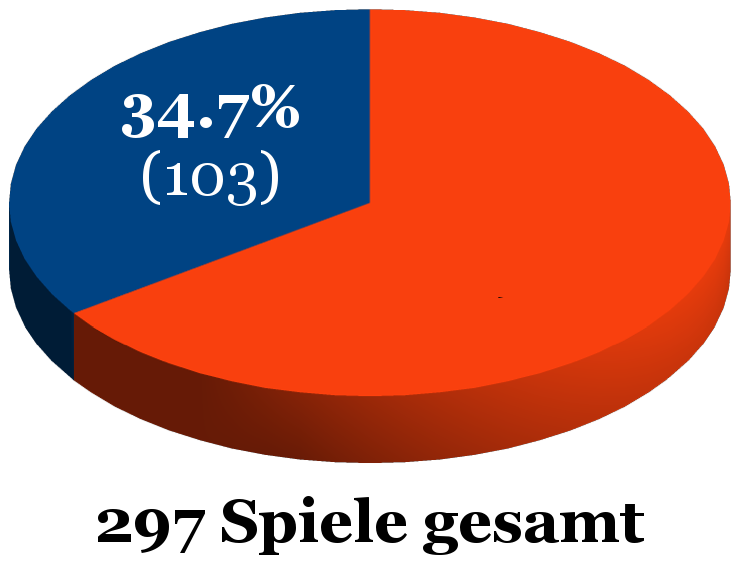
Anteil der Spiele, die in der Bundesliga bis zum 33. Spieltag mit einem Tor Unterschied gewonnen wurden (2015/16)
Zwar ist klar, dass das Siegerteam längst in nicht all diesen Spielen einfach nur Glück gehabt hat – aber solche scharfen Trennlinien lassen sich ohnehin immer nur sehr schwer ziehen. Generell ist dennoch logisch, dass eine besonders hohe Anzahl von Spielen, die mit einem Tor Vorsprung gewonnen wurden, höchstwahrscheinlich auf ein gewisses Glück schließen lassen, und besonders viele mit einem Tor Abstand verlorene Spiele tendenziell auf Pech.
Schauen wir uns an, wie sich die Anzahl der gewonnenen und verlorenen Eintorspiele auf die Bundesligateams verteilt, sortiert nach dem Saldo:
| Verein | +1 Siege | -1 Niederlagen | Saldo |
|---|---|---|---|
| Bayern München | 8 | 1 | +7 |
| Eintracht Frankfurt | 7 | 4 | +3 |
| Hertha Berlin | 7 | 4 | +3 |
| Schalke | 7 | 4 | +3 |
| Bayer Leverkusen | 9 | 6 | +3 |
| Dortmund | 5 | 2 | +3 |
| Darmstadt | 6 | 5 | +1 |
| Wolfsburg | 5 | 4 | +1 |
| Mainz | 7 | 7 | +/-0 |
| 1. FC Köln | 5 | 5 | +/-0 |
| Augsburg | 6 | 6 | +/-0 |
| Hoffenheim | 6 | 6 | +/-0 |
| Ingolstadt | 6 | 7 | |
| B. Mönchengladbach | 4 | 8 | |
| VfB Stuttgart | 2 | 6 | |
| Hamburger SV | 5 | 10 | |
| Werder Bremen | 3 | 8 | |
| Hannover | 5 | 10 |
Eine Maßzahl für die optimale Torverteilung erstellen
Die obige Tabelle ist zwar kein schlechter Indikator, hat aber einen wichtigen Nachteil: Für den VfB Stuttgart beispielsweise ist der Zufallssaldo von -4 eine schwerere Hypothek als für Borussia Mönchengladbach. Das liegt daran, dass Gladbach insgesamt deutlich mehr Punkte auf dem Konto hat, weswegen die in absoluten Zahlen identische Anzahl an Glückspunkten beim VfB relational stärker ins Gewicht fällt.
Ein Lösungsansatz ist in diesem Fall, den Zufallssaldo durch die Anzahl der Punkte zu teilen. Um bei einer intuitiv leserlicheren Maßzahl zu landen (die ich ab hier OTV+1 nenne) , habe ich das Ergebnis mit 100 multipliziert, was uns zu folgender Formel führt:
- OTV+1 = Saldo / Punktzahl * 100
Damit entsteht die folgende Tabelle, sortiert nach OTV+1 2:
| Verein | Saldo | OTV+1 |
|---|---|---|
| Eintracht Frankfurt | +3 | +8.33 |
| Bayern München | +7 | +8.24 |
| Hertha Berlin | +3 | +6.12 |
| Schalke | +3 | +6.12 |
| Bayer Leverkusen | +3 | +5.26 |
| Dortmund | +3 | +3.90 |
| Darmstadt | +1 | +2.63 |
| Wolfsburg | +1 | +2.38 |
| Mainz | +/-0 | +/-0 |
| 1. FC Köln | +/-0 | +/-0 |
| Augsburg | +/-0 | +/-0 |
| Hoffenheim | +/-0 | +/-0 |
| Ingolstadt | ||
| B. Mönchengladbach | ||
| VfB Stuttgart | ||
| Hamburger SV | ||
| Werder Bremen | ||
| Hannover |
Misst OTV+1 auch wirklich Glück und Pech?
Tatsächlich spricht einiges dafür. Wenn du diese Tabelle mit der Wett-Tabelle der Bundesliga nach dem 33. Spieltag vergleichst, werden dir einige Gemeinsamkeiten auffallen. Ich habe mit Hilfe von Libre Calc die Korrelation beider Tabellen gemessen3, und komme dabei auf einen (gerundeten) Koeffizienten von 0.47 – eine erstaunlich hohe Zahl, wenn man berücksichtigt, dass beide Tabellen auf sehr unterschiedliche Weise berechnet werden.
Das deutet wiederum darauf hin, dass es tatsächlich klare Überschneidungen gibt, was die Annahme bestärkt, dass mit beiden Methoden tatsächlich erfolgreich Zufall gemessen wird. Gleichzeitig gibt es auch genug Unterschiede, was darauf hoffen lässt, dass sich beide Messungen gegenseitig verbessern können.
Verbesserungspotential
Dass Verbesserungspotential besteht, kann man insbesondere an der Platzierung von Bayern München erkennen. Das Team ist ein Paradebeispiel dafür, dass ein Eintorsieg eher mit Pech zu tun haben kann als mit Glück – dennoch bliebe OTV+1 selbst bei einer eher ungünstigen Verteilung aussagekräftig, weil der Unterschied zwischen einem Unentschieden und einem Eintorsieg bei zwei Punkten liegt, während ein Zweitoreabstand keinen Punktvorteil bietet gegenüber einem Eintorabstand.
Ein vielversprechender Ansatz bei der Bewertung von Eintorsiegen dürfte die leicht zu ermittelnde Anzahl von Torschüssen sein. Genau dieser Blickwinkel würde es auch ermöglichen, Unentschieden und Siege mit einem Abstand von zwei Toren in die Messung einzubeziehen.
Ansonsten liegt auch der Verdacht nahe, dass eine Reihe von Siegen mit einem Abstand von zwei Toren qualitativ eher wie Eintorsiege zu sehen sind, insbesondere wenn der zweite Treffer eher spät im Spielverlauf erzielt wurde.
Fußnoten:
1 Grundsätzlich fallen solche Verteilungen bei Ereignissen mit kleinen Wahrscheinlichkeiten immer extremer aus als sonst.
2 Der einzige Unterschied in der Reihenfolge mit OTV+1 im Verhältnis zum Saldo: Eintracht Frankfurt und Bayern tauschen die Plätze.
3 Korrelationskoeffizienten können einen Wert zwischen -1 und +1 annehmen. Positive Korrelationen zeigen einen „je mehr desto mehr“-Zusammenhang, negative einen „je mehr desto weniger“-Zusammenhang. Ein Koeffizient nahe Null bedeutet, dass kein oder fast kein nennenswerter Zusammenhang besteht.
 RSS-Feed
RSS-Feed