Wirtschaftsjournalist vs Politik-Wettquoten
Auf Twitter bin ich am Sonntag über folgenden Tweet eines Wirtschaftsjournalisten der WELT gestoßen, es ging dabei um die von Ladbrokes geschätzten Chancen verschiedener möglicher Kanzlernachfolger:
Wer wird nächster Kanzler?
— Olaf Gersemann (@OlafGersemann) May 24, 2020
Chancen abgeleitet aus Wettquoten beim führenden Londoner Buchmacher @Ladbrokes.@welt pic.twitter.com/69TKVRMaOi
Zwar hat Olaf Gersemann freundlicherweise die Wettquoten in Wahrscheinlichkeiten übersetzt, vermutlich weil sein Publikum mit den Zahlen sonst (verständlicherweise) wenig anfangen könnte. Allerdings unterlaufen ihm auch ein paar Fehler. Manche davon sind offensichtlich, manche weniger.
- Die addierten Wahrscheinlichkeiten ergeben aufgrund der Buchmachermarge 112%. Das erhaltene Ergebnis ergibt damit zwar auf Wettebene Sinn[1], aber nicht wenn es um reale Wahlchancen geht.
- Er hat also vergessen, das Ergebnis auf 100% zu normalisieren. Beziehungsweise nicht gewusst, wie das geht.
- Auch eine Normalisierung auf 100% ergibt dabei noch nicht zwingend eine genaues Bild der Lage. Woran das im Detail liegt, erklärt der Rest dieses Blogposts.
Gehen wir alle nötigen Schritte für eine korrekte Interpretation der Ladbrokes-Quoten einmal genau durch:
Umwandlung der Wettquoten in Wahrscheinlichkeiten
Hier sind die Wettquoten, wie sie Ladbrokes im fraktionalen Format präsentiert (Siehe auch: Wie berechnen sich Wettquoten? - Wie Quoten funktionieren: 3. fraktionale Quoten):
Diese fraktionalen Wettquoten rechnest du nun in Dezimalquoten um, diese dann in prozentuale Wahrscheinlichkeiten, und schließlich kommt der Schritt, den Gersemann unterlassen hat: Du normalisierst die Wettquoten. Im Ergebnis sieht das so aus – und führt zu Wahrscheinlichkeiten, die aufaddiert 100% ergeben:
| Kandidat | Zähler | Nenner | dezimal | in % | % normalisiert |
|---|---|---|---|---|---|
| Markus Söder | 11 | 10 | 2.10 | 47.62% | 42.59% |
| Armin Laschet | 4 | 1 | 5.00 | 20.00% | 17.89% |
| Robert Habeck | 6 | 1 | 7.00 | 14.29% | 12.78% |
| Norbert Röttgen | 12 | 1 | 13.00 | 7.69% | 6.88% |
| Friedrich Merz | 7 | 2 | 4.50 | 22.22% | 19.87% |
| Marge | - | - | - | 111.82% | 100.00% |
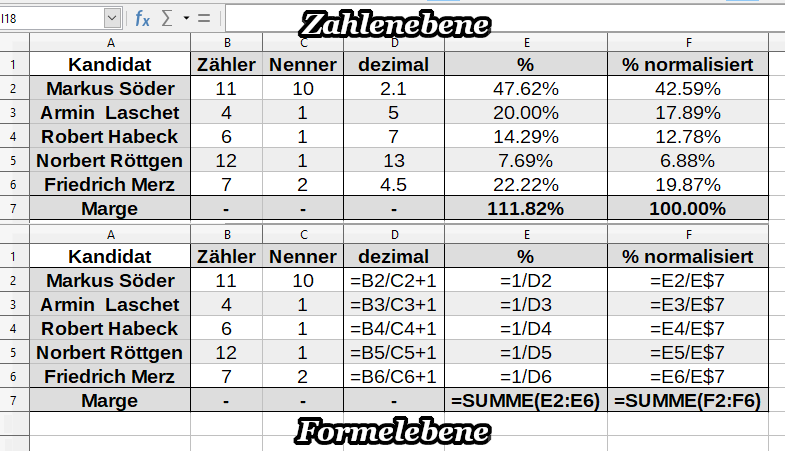
Für eine Normalisierung auf 100% teilst du also schlicht alle Wahrscheinlichkeiten durch die summierte Gesamtwahrscheinlichkeit (in diesem Fall also durch 111.82%). In einem Spreadsheet kannst du das folgendermaßen lösen:
Die Interpretation der Marge
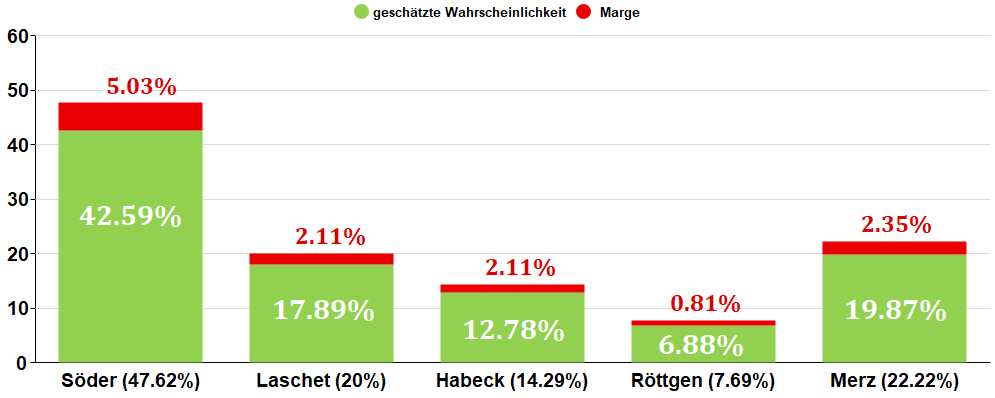
Allerdings gibt es auch mit diesen normalisierten Wahrscheinlichkeiten ein Problem: Sie repräsentieren nicht unbedingt, was der Buchmacher wirklich denkt. Der Grund dafür ist die Marge, die dem Buchmacher einiges an Spielraum gibt. Die soeben errechneten auf 100% normaliserten Quoten nehmen implizit an, dass der Buchmacher seine Marge auf alle Kandidaten gleichermaßen verteilt hat, proportional zu ihrem Wahrscheinlichkeitsanteil. Visuell kannst du dir das so vorstellen:
Was, wenn der Buchmacher für einen Kandidaten keine Marge einbaut?
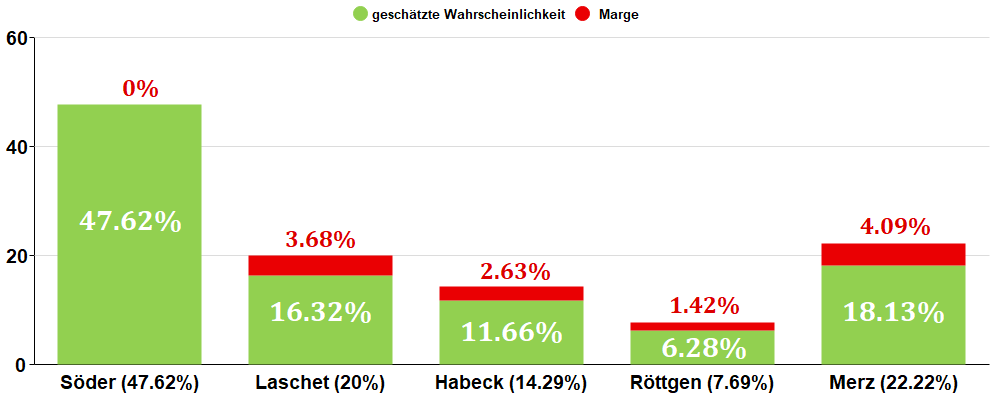
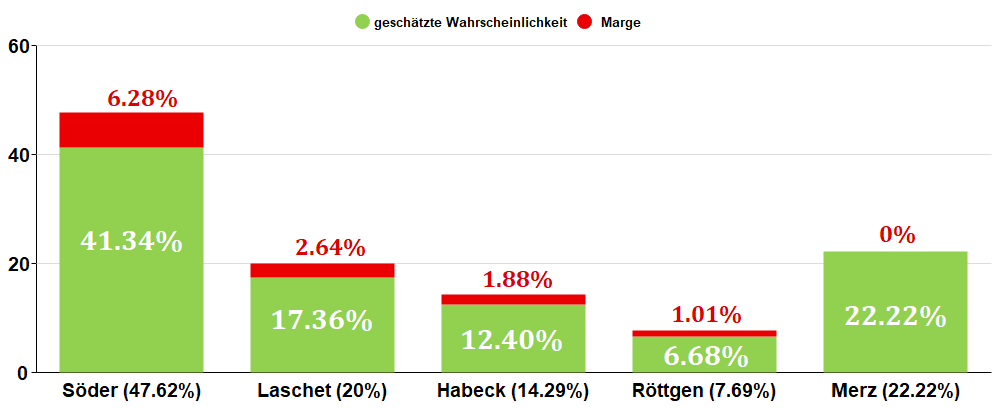
Es ist aber durchaus möglich, dass der Buchmacher nicht für jeden Kandidaten eine Marge verwendet[2] (etwa als Lockangebot). Beispielsweise ist es denkbar, dass Ladbrokes für den Favoriten gar keine Marge eingebaut und sie stattdessen proportional auf die übrigen Kandidaten verteilt hat:
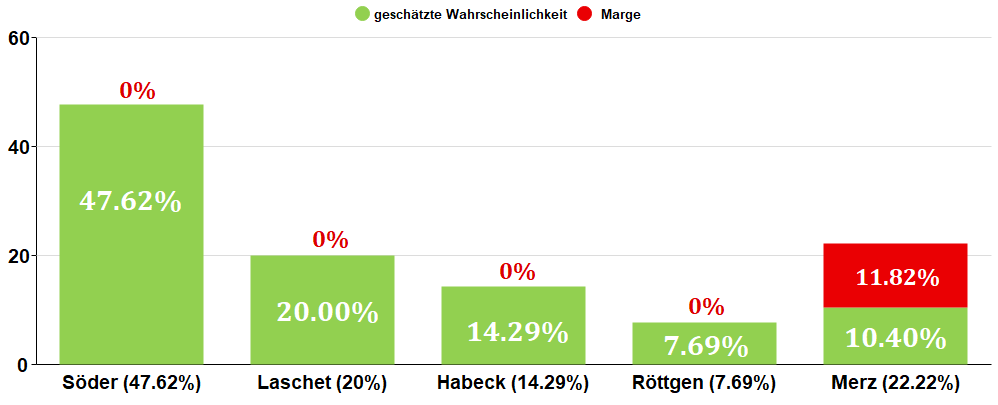
Prinzipiell ist das natürlich für jeden Kandidaten möglich, hier noch einmal mit Merz als Beispiel:
Margenverteilung, wenn es für einen Kandidaten keine Marge gibt: Spreadsheet
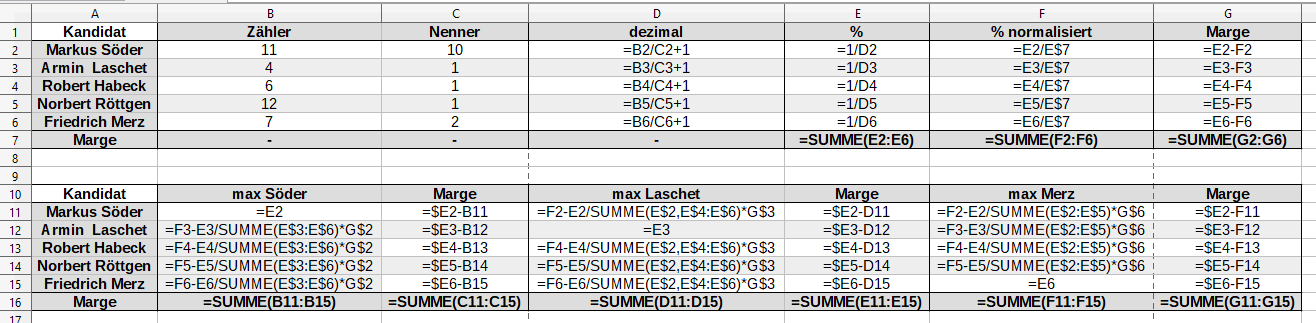
In einem Spreadsheet kannst du das folgendermaßen darstellen:
Was, wenn der Buchmacher nur für einen Kandidaten eine Marge einbaut?
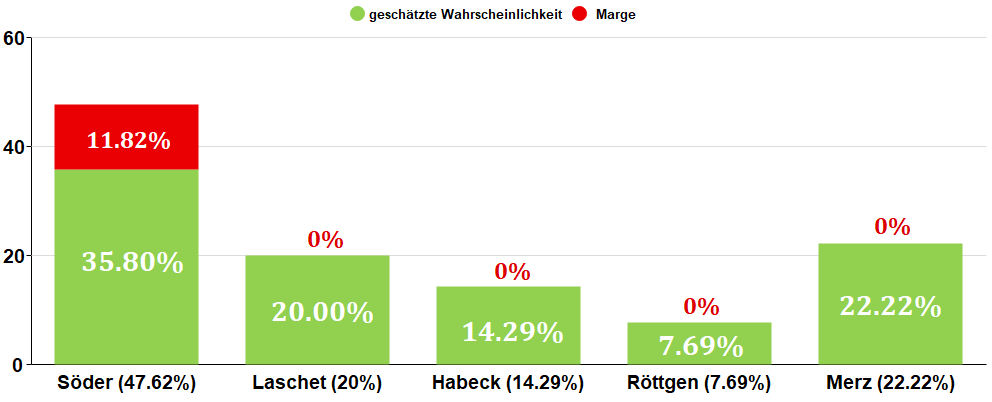
Es ist durchaus auch möglich, dass der Buchmacher lediglich für einen Kandidaten eine Marge einbaut, und für die übrigen Wettmöglichkeiten faire Wettquoten anbietet. Falls Ladbrokes beispielsweise nur für Söder eine Marge eingebaut haben sollte, sähe die realistische Einschätzung der Wahrscheinlichkeiten aller Kandidaten grundlegend anders aus:
In dem Fall wären also die meisten Wahrscheinlichkeitseinschätzungen von Ladbrokes für bare Münze zu nehmen, die für Söder läge aber weit daneben. Und so sieht die Einschätzung der wahren Wahrscheinlichkeiten aus, falls Ladbrokes die Marge ausschließlich für Merz verwendet:
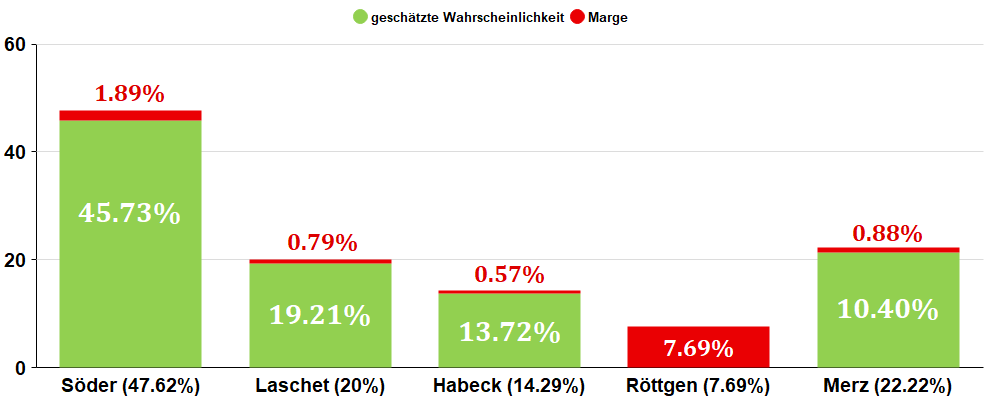
Margen-Sonderfall Röttgen
Ein interessanter Sonderfall tritt dabei ein, falls Außenseiter Röttgen das vorrangige Ziel der Marge wird: Seine Wettquote ist so hoch (und damit die davon implizierte Wahrscheinlichkeit so niedrig), dass die Schätzung für ihn von der Marge komplett aufgefressen wird, und sogar noch etwas für die anderen Kandidaten übrig bleibt:
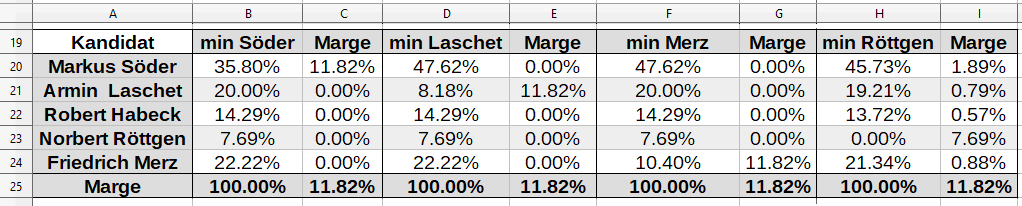
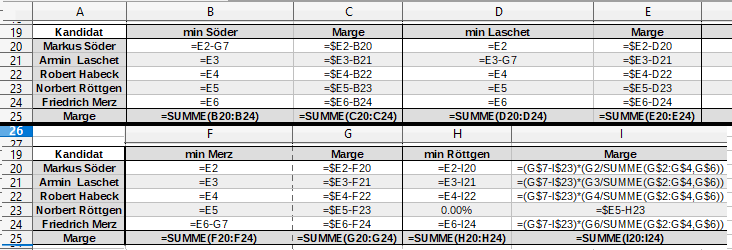
So sieht das im Spreadsheet aus
In einem Spreadsheet kannst du das folgendermaßen darstellen:
Hier kannst du den Spreadsheet herunterladen (Libre Office-Format):
| wetten-deutscher-kanzler.ods |
Fazit: Die Wahrscheinlichkeiten sind viel unsicherer, als sie ausehen
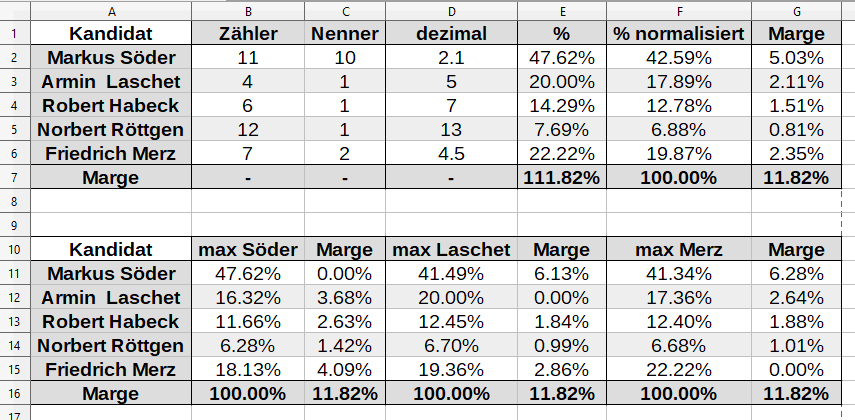
Mit all diesen Rechnungen ergibt sich folgendes Bild für die minimalen und maximalen Wahrscheinlichkeitsschätzungen auf Basis der Buchmacherquoten:
| Kandidat | minimal | maximal |
|---|---|---|
| Markus Söder | 35.80% | 47.62% |
| Armin Laschet | 8.18% | 20.00% |
| Robert Habeck | 2.47% | 14.29% |
| Norbert Röttgen | 0.00% | 7.69% |
| Friedrich Merz | 10.40% | 22.22% |
Um es höflich auszudrücken: Das sind enorme Spannbreiten für jeden einzelnen Kandidaten, die in der Summe kein sonderlich aussagekräftiges Bild ergeben. Was natürlich maßgeblich mit der exorbitanten Marge zu tun hat, die Ladbrokes seinen Kunden abverlangt.
Fußnoten:
[1] Die Wettquote dient in erster Linie dazu, dir deinen möglichen Gewinn zu verdeutlichen. Die implizierte Wahrscheinlichkeit der Wettquote dient als Schwellenwert, der dir sagt: So oft musst du prozentual ausgedrückt deine Wette mindestens gewinnen, um auf Dauer keine Verluste zu machen.
[2] Das kann verschiedene Gründe haben. Beispielsweise wird häufig auf Favoriten überproportional gewettet, und nicht selten spielt bei Politikwetten auch der Bekanntheitsgrad der Personen eine große Rolle. Entsprechend ist es nicht abwegig, dass Ladbrokes gerade bei Söder und Merz eine größere Marge einbaut, als proportional gerechtfertigt wäre – und entsprechend bei anderen Kandidaten wenig bis keine.

 RSS-Feed
RSS-Feed