Bevor ich mit dem neuen Zufallsindikator OTV-MiF weitermache, möchte ich zuerst dazu übergehen, statt der beschriebenen Quotienten zum Vergleich der Zufallsindikatoren untereinander den sogenannten Z-Wert (Z-Score im Englischen) einzuführen. Der Z-Wert funktioniert sehr ähnlich, beschreibt aber genau, wie viele Standardabweichungen der entsprechende Wert über oder unter dem Mittelwert liegt.
Um den Z-Wert für die Zufallsindikatoren zu berechnen, benötigst du folgende Komponenten:
- x - den Messwert für das Team bzw. die anstehende Paarung
- μ – das arithmetische Mittel der Gesamtpopulation[1], also aller Teams bzw. Paarungen
- σ - die Standardabweichung der Gesamtpopulation[2], also aller Teams bzw. Paarungen
Diese Werte fügst du nun in folgende Formel ein, um den Z-Wert zu berechnen:
Praktisches Beispiel: Führungsminuten der WM-Teams
Ich habe die Führungsminuten der WM-Teams aus den Qualifikationsspielen erhoben (weshalb Russland außen vor bleibt), wobei ich maximal die letzten 5 Spiele berücksichtigt habe, und keinerlei Spiele, die vor Juli 2017 stattgefunden haben. Im Schnitt pro Spiel ergibt sich folgendes Bild:
| Rang | Team | Gruppe | Führungsminuten (Schnitt) |
|---|---|---|---|
| 1 | Deutschland | F | |
| 2 | Spanien | B | |
| 3 | Schweden | F | |
| 4 | Frankreich | C | |
| 5 | Portugal | B | |
| 6 | Belgien | G | |
| 7 | Marokko | B | |
| 8 | Dänemark | D | |
| 9 | Polen | H | |
| 10 | Nigeria | D | |
| 11 | Schweiz | E | |
| 12 | Australien | C | |
| 13 | Serbien | E | |
| 14 | Kroatien | D | |
| 15 | England | G | |
| 16 | Senegal | H | |
| 17 | Ägypten | A | |
| 18 | Mexiko | F | |
| 19 | Island | C | |
| 20 | Brasilien | E | |
| 21 | Argentinien | C | |
| 22 | Uruguay | A | |
| 23 | Japan | H | |
| 24 | Kolumbien | H | |
| 25 | Peru | D | |
| 26 | Costa Rica | E | |
| 27 | Tunesien | G | |
| 28 | Südkorea | F | |
| 29 | Saudi-Arabien | A | |
| 30 | Iran | B | |
| 31 | Panama | G | |
| - | - | Standardabweichung: | |
| - | - | Mittelwert: |
Beispielsweise wäre für Deutschland die Rechnung also folgende:
- (72.00 – 25.67) / 22.39 = 46.33 / 22.39 ≈ 2.07
- (17.50 – 25.67) / 22.39 = -8.17 / 22.39 ≈ -0.36
Für alle Teams ergeben sich demnach folgende (auf die zweite Nachkommastelle gerundeten) Z-Werte:
| Rang | Team | Gruppe | Führungsminuten (Schnitt) | Z-Wert (σ) |
|---|---|---|---|---|
| 1 | Deutschland | F | ||
| 2 | Spanien | B | ||
| 3 | Schweden | F | ||
| 4 | Frankreich | C | ||
| 5 | Portugal | B | ||
| 6 | Belgien | G | ||
| 7 | Marokko | B | ||
| 8 | Dänemark | D | ||
| 9 | Polen | H | ||
| 10 | Nigeria | D | ||
| 11 | Schweiz | E | ||
| 12 | Australien | C | ||
| 13 | Serbien | E | ||
| 14 | Kroatien | D | ||
| 15 | England | G | ||
| 16 | Senegal | H | ||
| 17 | Ägypten | A | ||
| 18 | Mexiko | F | ||
| 19 | Island | C | ||
| 20 | Brasilien | E | ||
| 21 | Argentinien | C | ||
| 22 | Uruguay | A | ||
| 23 | Japan | H | ||
| 24 | Kolumbien | H | ||
| 25 | Peru | D | ||
| 26 | Costa Rica | E | ||
| 27 | Tunesien | G | ||
| 28 | Südkorea | F | ||
| 29 | Saudi-Arabien | A | ||
| 30 | Iran | B | ||
| 31 | Panama | G | ||
| - | - | Standardabweichung: | ||
| - | - | Mittelwert: |
Was der Z-Wert bedeutet
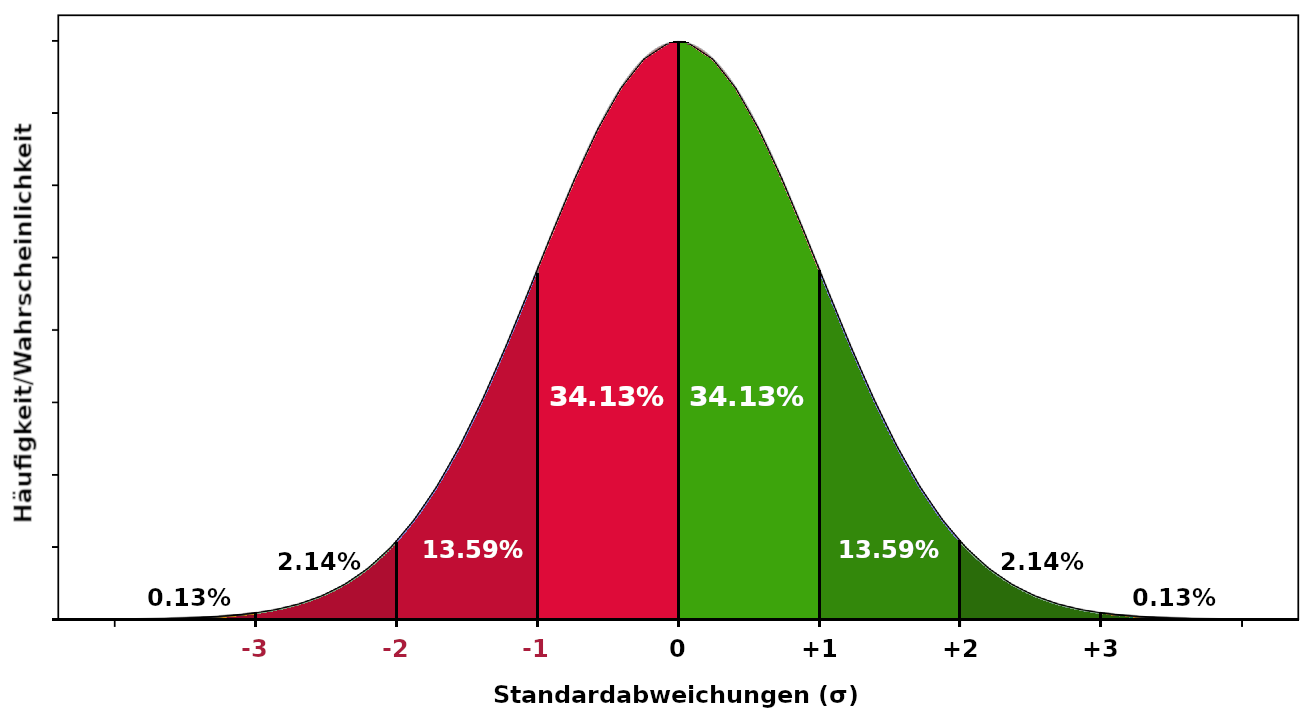
Wie bereits erwähnt drückt der Z-Wert in diesem Fall aus, wie viele Standardabweichungen das betreffende Team vom Durchschnitt entfernt ist. Aber was sagt das darüber aus, wie häufig oder selten der entsprechende Wert ist? Das zeigt dir diese Grafik:
Daran kannst du erkennen, dass etwas mehr als 68% aller auftretenden Werte (eine Normalverteilung vorausgesetzt) in den Bereich fallen, der eine Standardabweichung von der Null entfernt ist. Danach wird die Luft schon deutlich dünner, und entsprechend bemerkenswert sind die Werte von Deutschland und Panama. Ein Abstand von 3 oder mehr Standardabweichungen kommt dagegen nur sehr selten vor.
Fall du die exakten Zahlen benötigst, findest du hier eine ausführliche Tabelle.
Fußnoten:
[1] In Libre Calc verwendest du dazu einfach die MITTELWERT-Formel.
[2] In Libre Calc verwendest du in diesem Fall die Formel STABW.N – dies aber nur, wenn dir alle Werte der Population bekannt sind. Im Falle einer Stichprobe müsstest du STABW verwenden. Es wird etwas anders gerechnet in diesem Fall, weshalb die Unterscheidung wichtig ist.

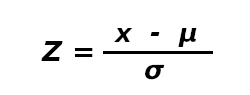
 RSS-Feed
RSS-Feed