Wenn dein Wettmodell dir (wie im letzten Blogpost der Wettmodellserie beschrieben) die mittleren zu erwartenden Werte für Torüberlegenheit und Gesamttorzahl für jede Partie anzeigt, kannst du diese Werte mit denen des Buchmachers vergleichen – sowohl für das Asiatische Handicap, als auch die Gesamttoranzahl (Over/Under).
Dazu benötigst du allerdings die Handicap- und Torwerte, die der Buchmacher für die 50%-Linie veranschlagt, damit sie mit deinen Werten exakt vergleichbar sind. Meist aber bietet der Buchmacher für jede Linie nur Quoten ober- oder unterhalb von 2.00, also was tun?
Ich zeige dir am Beispiel der Partie Hamburg gegen Leverkusen, wie du diese Werte mit ein wenig Algebra leicht berechnen kannst, ausgehend von den Wettquoten, die Pinnacle für diese Partie anbietet.
Schritt 1: Finde die beiden Handicaps, deren Quoten am nächsten an 50% (2.00) liegen
Für die Partie Hamburg gegen Leverkusen am 17. Februar 2018 habe ich beim Schreiben dieser Zeilen folgende Wettquoten vorgefunden, die am nächsten an 2.00 waren:
| Wette | Linie 1 | Quote | Linie 2 | Quote |
|---|---|---|---|---|
| Hamburg | 1.833 | 2.13 | ||
| Leverkusen | 2.09 | 1.806 | ||
| Over | 2.04 | 1.781 | ||
| Under | 1.862 | 2.14 |
Schritt 2: Normalisiere die Wettquoten auf 100% (Herausrechnen der Buchmachermarge)
Um die Buchmachermarge herauszurechnen, berechnest du zuerst die implizierten Wahrscheinlichkeiten der Wettquoten (1/Quote). Dann teilst du diese beiden implizierten Wahrscheinlichkeiten jeweils durch die Summe beider Wahrscheinlichkeiten[1].
| Heimhandicap | Hamburg (Heim) | 1/Quote | Leverkusen (Gast) | 1/Quote | Summe (H+G) |
|---|---|---|---|---|---|
| AHC +0.50 | 1.833 | 0.546 | 2.090 | 0.478 | 1.024 |
| +0.5 normalisiert | 1/Quote/Summe: | 0.533 | 1/Quote/Summe: | 0.467 | 1.000 |
| AHC +0.25 | 2.130 | 0.469 | 1.806 | 0.554 | 1.023 |
| +0.25 normalisiert | 1/Quote/Summe: | 0.459 | 1/Quote/Summe: | 0.541 | 1.000 |
| O/U-Linie | Over | 1/Quote | Under | 1/Quote | Summe (O+U) |
|---|---|---|---|---|---|
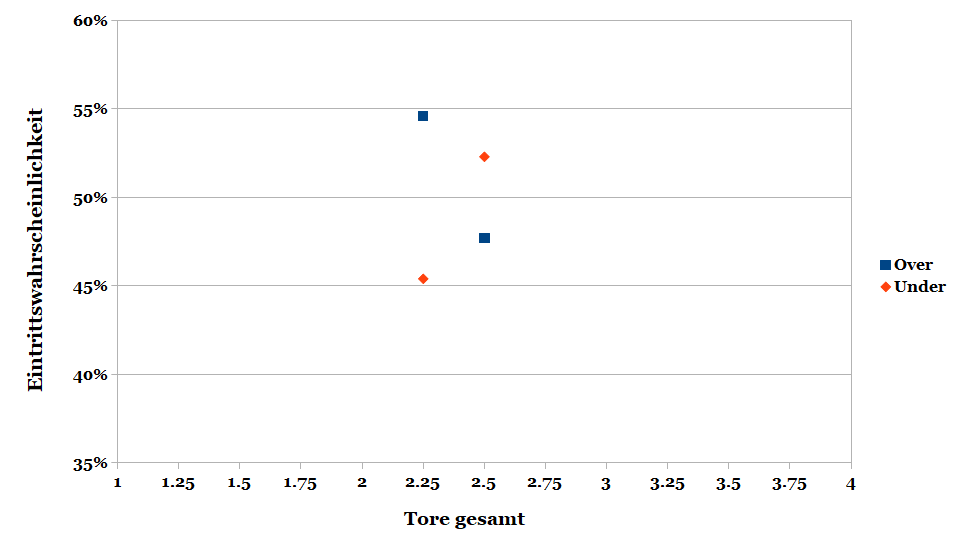
| 2.50 | 2.040 | 0.490 | 1.862 | 0.537 | 1.027 |
| 2.50 normalisiert | 1/Quote/Summe: | 0.477 | 1/Quote/Summe: | 0.523 | 1.000 |
| 2.25 | 1.781 | 0.561 | 2.140 | 0.467 | 1.029 |
| 2.25 normalisiert | 1/Quote/Summe: | 0.546 | 1/Quote/Summe: | 0.454 | 1.000 |
Exkurs: Sich die Wahrscheinlichkeiten im Bezug zur Gesamttoranzahl grafisch vorstellen
Deine normalisierten Wahrscheinlichkeiten kannst du dir auch grafisch vorstellen, für die Gesamttorwerte sähe das beispielsweise so aus:
Durch diese beiden Punkte ziehst du eine Linie, und ermittelst für diese Gerade die mathematisch korrekte Formel. Dann berechnest du, an exakt welchem Punkt (in Toren ausgedrückt) die Gerade die 50%-Linie schneidet. Für Geraden wird immer die Formel y = mx + n verwendet[2] , weshalb du zuerst das m (die Steigung) berechnest, und dann den Rest ermittelst.
Schritt 3: Die Steigung der Geraden berechnen
Für das Under kennst du diese beiden Punkte:
| Under | Punkt 1 | Punkt 2 |
|---|---|---|
| Tore (x) | 2.25 | 2.5 |
| Wahrscheinlichkeit (y) | 0.454 | 0.523 |
Diese setzt du in folgende Formel ein und berechnest dann die Steigung m:
Es ist in diesem Zusammenhang übrigens egal, welchen Punkt du von welchem abziehst, das Ergebnis ist dasselbe.
Schritt 4: Die Funktion der Geraden berechnen
Für das Berechnen der Funktion benötigst du jetzt lediglich einen der beiden Punkte (welcher ist egal), und die eben errechnete Steigung. In diesem Beispiel habe ich Punkt 1 (das Under 2.25) und die Steigung m (0.276) in die folgende Formel eingesetzt:
Schritt 5: Für 50% auflösen
Jetzt musst du nur noch für y die gewünschte Wahrscheinlichkeit einsetzen und die Gleichung nach x auflösen. Da du herausfinden willst, welchen Wert x bei 50% annimmt, setzt du für y 0.5 ein:
In diesem Fall erwartet der Buchmacher also im Mittel 2.417 Tore für dieses Spiel. Wenn dein Modell signifikant darüber liegen sollte, signalisiert das also eine Overwette – und eine Underwette, wenn es signifikant darunter liegt.
Ausblick
In Teil 1c erkläre ich dir, wie du diese Berechnungen in einen Spreadsheet einfügst, damit du die Werte nicht jedes Mal erneut von Hand berechnen musst.
Fußnoten:
[1] Als Formel für das Over ausgedrückt: (1/Overquote) / (1/Overquote + 1/Underquote) – entsprechend (1/Underquote) / (1/Overquote + 1/Underquote) für das Under.
[2] Es ist nicht zwingend zu 100% korrekt, eine Gerade zu verwenden, weil Tore keinem exakt linearen Zusammenhang folgen. Da wir aber die Werte nehmen, die am nächsten an der 50%-Grenze liegen, reicht das als Annäherung vollkommen aus.

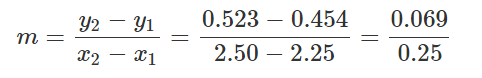
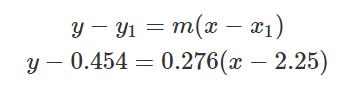
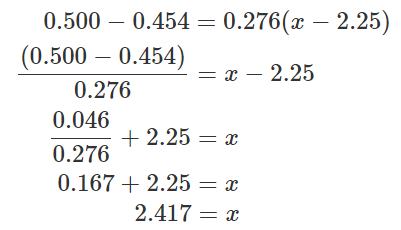
 RSS-Feed
RSS-Feed